28 Majority Preference
Given an (anonymous) profile \(\mathbf{P}\), we are interested in evaluating how well the candidates performed in the election. One straightforward way to measure the performance of a candidate is by counting how many voters rank that candidate in first place.
For example, consider the following anonymous profile for three candidates \(\{a, b, c\}\):
\[\begin{array}{ccc} 34 & 33 & 33\\\hline a & b & c\\ b & c & b\\ c & a & a\\ \end{array}\]From this profile:
- \(34\) voters rank \(a\) in first place.
- \(33\) voters rank \(b\) in first place.
- \(33\) voters rank \(c\) in first place.
Based on this measure, \(a\) appears to perform the best, with 34 voters ranking \(a\) first. However, this measure fails to account for an important detail: a significant majority of voters (66) rank \(a\) last!
If \(a\) is not the “best” candidate, we are left with \(b\) and \(c\). Both candidates receive \(33\) first-place rankings, resulting in a tie based on first-place votes. To break the tie, we can examine the voters’ preferences between \(b\) and \(c\): \(67\) voters (\(34 + 33\)) rank \(b\) above \(c\), while only \(33\) voters rank \(c\) above \(b\). Therefore, considering the overall preferences, \(b\) is the clear winner.
This example highlights a significant flaw in the Plurality voting method: Plurality—which selects \(a\) as the winner in this example—may elect a candidate who is ranked last by a majority of voters. In particular, this implies that there is another candidate whom a majority of voters rank above the winning candidate \(a\).
Similarly, other voting methods, such as Instant Runoff, can suffer from related issues. Consider the following profile:
\[\begin{array}{ccc} 40 & 45 & 15\\\hline b & a & c\\ c & c & b\\ a & b & a \end{array}\]There is no absolute majority winner in this profile. According to the Instant Runoff voting method, the candidate with the fewest first-place votes is eliminated. In this case, \(c\) is removed since they are ranked first by only \(15\) voters, compared to \(40\) voters for \(b\) and \(45\) voters for \(a\).
After \(c\) is eliminated, candidate \(b\) becomes the winner, as they are ranked first by \(40 + 15 = 55\) voters in the reduced profile. However, choosing \(b\) as the winner disregards the preferences of a majority of voters. Specifically, \(45 + 15 = 60\) voters rank \(c\) above \(b\), while only \(40\) voters rank \(b\) above \(c\). Thus, \(c\) is ranked above \(b\) by a majority of voters. To highlight this issue, the original profile is reproduced below, focusing on the voters’ rankings of \(b\) and \(c\):
\[\begin{array}{ccc} 40 & 45 & 15\\\hline \cellcolor{red}{\textcolor{white}{b}} & a & \cellcolor{blue}{\textcolor{white}{c}}\\ \cellcolor{blue}{\textcolor{white}{c}} & \cellcolor{blue}{\textcolor{white}{c}} & \cellcolor{red}{\textcolor{white}{b}}\\ a & \cellcolor{red}{\textcolor{white}{b}} & a \end{array}\]Like the Plurality voting method, Instant Runoff may elect a candidate who is ranked lower than another candidate by a majority of voters. In this case, \(b\) is elected even though a majority of voters rank \(c\) above \(b\).
A real-life example of this phenomenon occurred during the 2022 special general election in Alaska, which used Instant Runoff Voting. In this election, a majority of voters preferred Nick Begich over the winning candidate, Mary Peltola. For more details, see the analysis at https://github.com/voting-tools/election-analysis/blob/main/alaska_2022.ipynb for details.
In this section, we define the majority preference of voters in an election as a tool for evaluating how candidates perform.
28.1 Margin of Victory
We begin by defining the margin of victory for each pair of candidates, which measures the number of voters who rank one candidate above the other in an election.
Definition 28.1 (Margin) Suppose that \(V\) is a set of voters and \(X\) is a set of candidates, and that \(\mathbf{P}\) is a profile for the pair \((V, X)\). For candidates \(x, y \in X\), the margin of \(x\) over \(y\) is the number of voters in \(\mathbf{P}\) who rank \(x\) above \(y\), minus the number of voters who rank \(y\) above \(x\). We write \(Margin_\mathbf{P}(x, y)\) for the margin of \(x\) over \(y\) in \(\mathbf{P}\). Formally, the margin of \(x\) over \(y\) is given by: \[Margin_\mathbf{P}(x, y) = |\{i\mid x\mathrel{\mathbf{P}_i} y\}| - |\{i\mid y\mathrel{\mathbf{P}_i} x\}|.\]
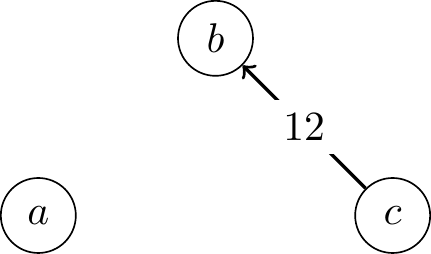
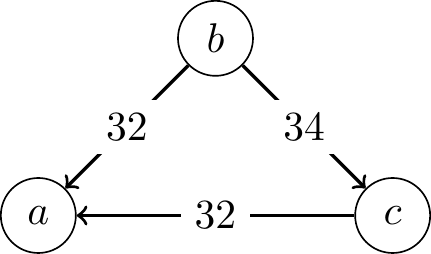
Let \(\mathbf{P}\) be the profile discussed above (repeated here for convenience):
\[\begin{array}{ccc} 34 & 33 & 33\\\hline a & b & c\\ b & c & b\\ c & a & a\\ \end{array}\]The margins of victory for each pair of candidates are as follows:
\[\begin{array}{rclcl} Margin_\mathbf{P}(a, b) & = & 34 - 66 & = & -32\\ Margin_\mathbf{P}(b, a) & = & 66 - 34 & = & 32\\[4pt] Margin_\mathbf{P}(a, c) & = & 34 - 66 & = & -32\\ Margin_\mathbf{P}(c, a) & = & 66 - 34 & = & 32\\[4pt] Margin_\mathbf{P}(b, c) & = & 67 - 33 & = & 34\\ Margin_\mathbf{P}(c, b) & = & 33 - 67 & = & -34\\ \end{array}\]Note that for any pair of candidates \(x\) and \(y\), we have: \[Margin_\mathbf{P}(x, y) = -Margin_\mathbf{P}(y, x).\] Additionally, the margin of a candidate over themselves is always zero: \[Margin_\mathbf{P}(x, x) = 0.\]
The margin of victory is a valuable tool for comparing the performance of candidates in an election. In particular, we say that \(x\) is majority preferred to \(y\) when more voters rank \(x\) above \(y\) than the other way around.
Definition 28.2 (Majority Preference) Suppose that \(V\) is a set of voters and \(X\) is a set of candidates, and that \(\mathbf{P}\) is a profile for the pair \((V, X)\). For candidates \(x, y \in X\), we say that \(x\) is majority preferred to \(y\) when \(Margin_\mathbf{P}(x, y) > 0\).
In the above profile \(\mathbf{P}\), we have the following:
- \(b\) is majority preferred to \(a\);
- \(b\) is majority preferred to \(c\); and
- \(c\) is majority preferred to \(a\).
28.2 Margin Graph
We visualize the margins of victory between candidates in a profile \(\mathbf{P}\) by listing all the candidates and drawing an edge from candidate \(x\) to candidate \(y\), labeled with the margin of \(x\) over \(y\), if \(x\) is majority preferred to \(y\). This visualization is called the margin graph of the profile \(\mathbf{P}\).
The margin graph for the following profile \(\mathbf{P}\) \[\begin{array}{ccc} 34 & 33 & 33\\\hline a & b & c\\ b & c & b\\ c & a & a\\ \end{array}\]is shown below:
We conclude this section with a few observations about the margin graph:
- The arrows in a margin graph indicate that candidate \(x\) is majority preferred to candidate \(y\) when there is an edge from \(x\) pointing to \(y\). Since \(x\) being majority preferred to \(y\) implies that \(y\) is not majority preferred to \(x\), there can be at most one edge between any two candidates in the margin graph.
- If there is an even number of voters, there may be a tie between two candidates \(x\) and \(y\), where \(Margin_\mathbf{P}(x, y) = 0\). In this case, no edge will appear between \(x\) and \(y\) in the margin graph.
- If there is an odd number of voters, then there must be a majority preference between any two candidates. In this case, the margin graph will contain an edge between every pair of candidates.
28.3 Exercises
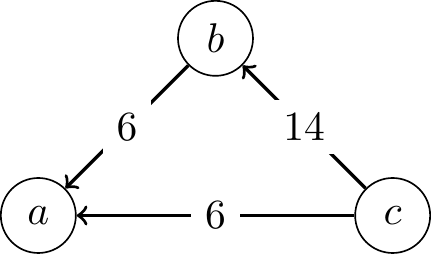
- In the following profile, find the margins of each pair of candidates and draw the margin graph.
Show Answer
- The margin of \(a\) over \(b\) is \(12 - 18 = -6\)
- The margin of \(b\) over \(a\) is \(18 - 12 = 6\)
- The margin of \(a\) over \(c\) is \(12 - 18 = -6\)
- The margin of \(c\) over \(a\) is \(18 - 12 = 6\)
- The margin of \(b\) over \(c\) is \(8 - 22 = -14\)
- The margin of \(c\) over \(b\) is \(22 - 8 = 14\)
The margin graph is:
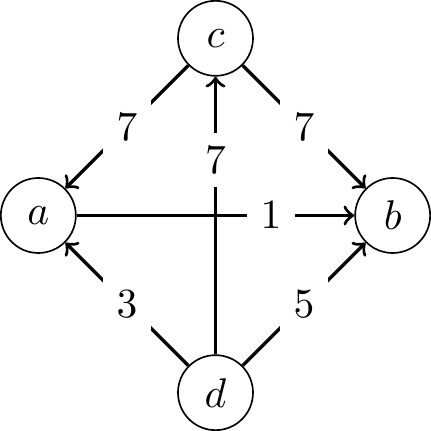
- In the following profile, find the margins of each pair of candidates and draw the margin graph.
Show Answer
- The margin of \(a\) over \(b\) is \(9 - 8 = 1\)
- The margin of \(b\) over \(a\) is \(8 - 9 = -1\)
- The margin of \(a\) over \(c\) is \(5 - 12 = -7\)
- The margin of \(c\) over \(a\) is \(12 - 5 = 7\)
- The margin of \(a\) over \(d\) is \(7 - 10 = -3\)
- The margin of \(d\) over \(a\) is \(10 - 7 = 3\)
- The margin of \(b\) over \(c\) is \(5 - 12 = -7\)
- The margin of \(c\) over \(b\) is \(12 - 5 = 7\)
- The margin of \(b\) over \(d\) is \(6 - 11 = -5\)
- The margin of \(d\) over \(b\) is \(11 - 6 = 5\)
- The margin of \(c\) over \(d\) is \(5 - 12 = -7\)
- The margin of \(d\) over \(c\) is \(12 - 5 = 7\)
The margin graph is:
- In the following profile, find the margins of each pair of candidates and draw the margin graph.
Show Answer
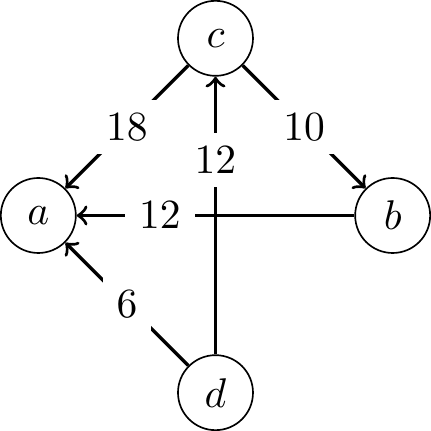
- The margin of \(a\) over \(b\) is \(6 - 18 = -12\)
- The margin of \(b\) over \(a\) is \(18 - 6 = 12\)
- The margin of \(a\) over \(c\) is \(3 - 21 = -18\)
- The margin of \(c\) over \(a\) is \(21 - 3 = 18\)
- The margin of \(a\) over \(d\) is \(9 - 15 = -6\)
- The margin of \(d\) over \(a\) is \(15 - 9 = 6\)
- The margin of \(b\) over \(c\) is \(7 - 17 = -10\)
- The margin of \(c\) over \(b\) is \(17 - 7 = 10\)
- The margin of \(b\) over \(d\) is \(12 - 12 = 0\)
- The margin of \(d\) over \(b\) is \(12 - 12 = 0\)
- The margin of \(c\) over \(d\) is \(6 - 18 = -12\)
- The margin of \(d\) over \(c\) is \(18 - 6 = 12\)
The margin graph is:
- In the following profile, find the margins of each pair of candidates and draw the margin graph.
Show Answer
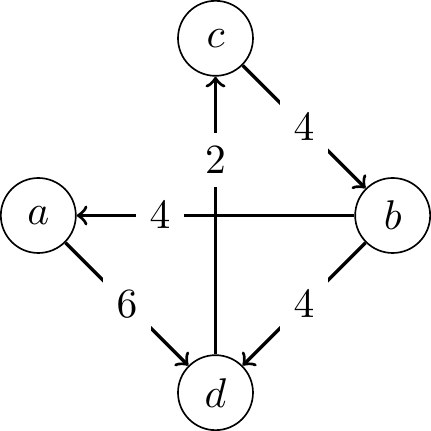
- The margin of \(a\) over \(b\) is \(7 - 11 = -4\)
- The margin of \(b\) over \(a\) is \(11 - 7 = 4\)
- The margin of \(a\) over \(c\) is \(9 - 9 = 0\)
- The margin of \(c\) over \(a\) is \(9 - 9 = 0\)
- The margin of \(a\) over \(d\) is \(12 - 6 = 6\)
- The margin of \(d\) over \(a\) is \(6 - 12 = -6\)
- The margin of \(b\) over \(c\) is \(7 - 11 = -4\)
- The margin of \(c\) over \(b\) is \(11 - 7 = 4\)
- The margin of \(b\) over \(d\) is \(11 - 7 = 4\)
- The margin of \(d\) over \(b\) is \(7 - 11 = -4\)
- The margin of \(c\) over \(d\) is \(8 - 10 = -2\)
- The margin of \(d\) over \(c\) is \(10 - 8 = 2\)
The margin graph is:
- In the following profile, find the margins of each pair of candidates and draw the margin graph.
Show Answer
- The margin of \(a\) over \(b\) is \(13 - 13 = 0\)
- The margin of \(b\) over \(a\) is \(13 - 13 = 0\)
- The margin of \(a\) over \(c\) is \(13 - 13 = 0\)
- The margin of \(c\) over \(a\) is \(13 - 13 = 0\)
- The margin of \(b\) over \(c\) is \(7 - 19 = -12\)
- The margin of \(c\) over \(b\) is \(19 - 7 = 12\)
The margin graph is: