26 Condorcet Consistent Voting Methods

A voting method is Condorcet consistent if it always selects only the Condorcet winner whenever one exists. In this section, we introduce three voting methods that satisfy this property. These methods elect the same winner when a Condorcet winner exists but may choose different winners when there is no Condorcet winner.

26.1 Copeland

Say that the win-loss record for a candidate \(x\) is the number of candidates that \(x\) is majority preferred to minus the number of candidates that is majority preferred to \(y\).

Any candidate with the largest win-loss record is a Copeland winner.

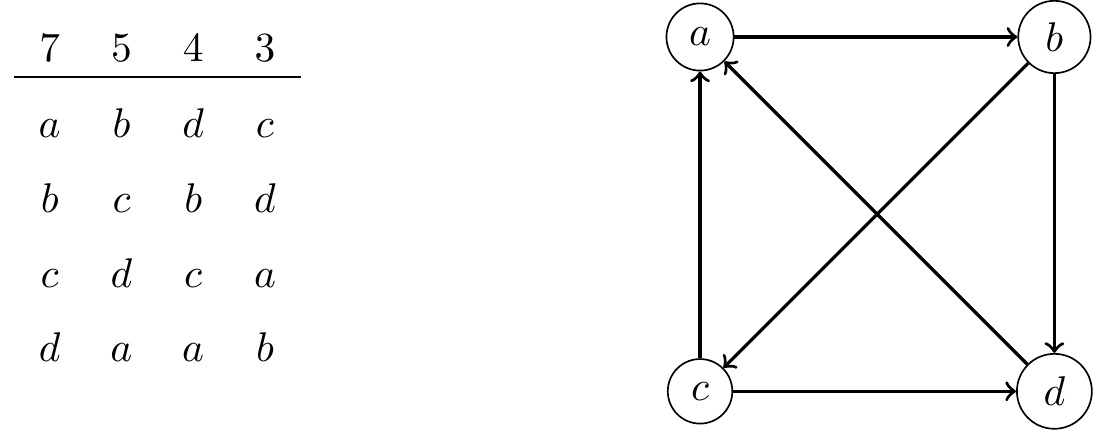
Consider the following election that produces the majority graph on the right:

To find the Copeland winners, calculate the win-loss records of each candidate:

The win-loss record of \(a\) is \(1-2=-1\) since \(a\) is majority preferred to \(b\) and both \(c\) and \(d\) are majority preferred to \(a\).
The win-loss record of \(b\) is \(2-1=1\) since \(b\) is majority preferred to both \(c\) and \(d\), and \(a\) is majority preferred to \(b\).
The win-loss record of \(c\) is \(2-1=1\) since \(c\) is majority preferred to both \(a\) and \(d\), and \(b\) is majority preferred to \(c\).
The win-loss record of \(d\) is \(1-2=-1\) since \(d\) is majority preferred to \(a\) and both \(b\) and \(c\) are majority preferred to \(d\).

Since \(b\) and \(c\) have the largest win-loss records, they are the Copeland winners.

26.2 Minimax

Consider the following margin graph for the top three candidates from the 2007 Glasgow City Council election (see https://github.com/voting-tools/election-analysis/blob/main/glasgow_govan_2007.ipynb for a detailed analysis of this election):

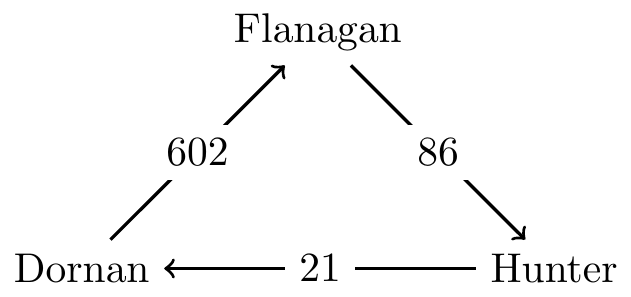
All candidates are tied according to Copeland, as each candidate’s win-loss record is 0. However, if we must select a single winner based on pairwise comparisons, Dornan clearly stands out as the best choice. Dornan has both the smallest head-to-head loss of 21 to Hunter and the largest head-to-head win of 602 over Flanagan.

To transform this observation into a voting method, we need to address two key questions:

What should we prioritize if no single candidate has both the smallest head-to-head loss and the largest head-to-head win—should we focus on minimizing losses or maximizing wins?
In elections with more than three candidates, a candidate may have multiple losses. How should we aggregate these losses to determine the winner?

The Minimax voting method addresses these questions as follows by focusing on identifying candidates that minimize their largest loss. It selects a winner as follows:

For each candidate, identify their largest head-to-head loss in the pairwise comparisons against every other candidate.
A candidate with the smallest largest loss is declared a Minimax winner.

Note that constructing the margin graph for the election is the most effective way to identify the Minimax winner. To illustrate, consider the following margin graph for an election with four candidates, where the largest loss for each candidate is highlighted:

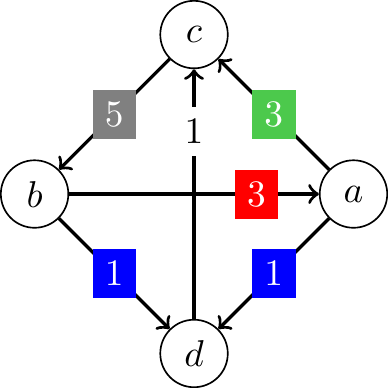
To find the Minimax winner, we identify the largest head-to-head loss for each candidate:

\(a\) loses to \(b\) by a margin of 3, so its largest loss is 3.
\(b\) loses to \(c\) by a margin of 5, so its largest loss is 5.
\(c\) loses to \(d\) by a margin of 1 and to \(a\) by a margin of 3, so its largest loss is 3.
\(d\) loses to \(b\) by a margin of 1 and to \(a\) by a margin of 1, so its largest loss is 1.

Since \(d\) has the smallest largest loss, \(d\) is the Minimax winner.

This example also highlights the difference between Minimax and Copeland. The Copeland winners are \(a\) and \(b\), as they have the largest win-loss records of 1.

26.3 Split Cycle

Consider the following margin graph for an election with four candidates:

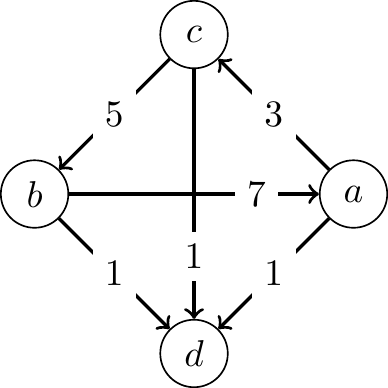
In this election, \(d\) is the Minimax winner because it has the smallest largest loss. However, it is worth noting that \(d\) is also the Condorcet loser, as it loses to all other candidates in head-to-head comparisons. The Copeland voting method makes a better choice in this election. The Copeland winners are \(a\), \(b\), and \(c\), as they each have the highest win-loss record of 1, while \(d\) has a win-loss record of \(-3\). However, Copeland completely ignores the margins of victory between candidates.

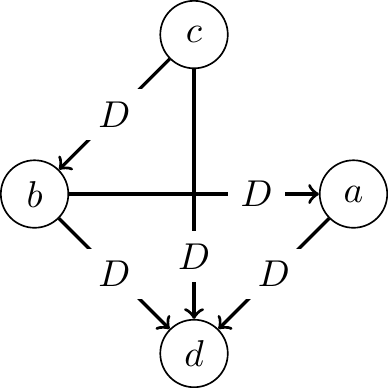
Split Cycle is a voting method that combines the strengths of both Minimax and Copeland. To determine the Split Cycle winners, follow these steps:

In each majority cycle, identify the wins with the smallest margin in that cycle.
After completing step 1 for all cycles, discard the identified wins. All remaining wins count as defeats.
The candidates that are not defeated by any other candidate are the Split Cycle winners.

In the margin graph above, there is one majority cycle: \(a, c, b\). The smallest margin in this cycle is 3, which corresponds to the margin of victory for \(a\) over \(c\). Since this margin is the smallest in the cycle, we discard this win. All remaining wins count as defeats.

The resulting graph is shown below, where each edge from one candidate to another is labeled with a \(D\) to indicate that the first candidate defeats the second candidate.

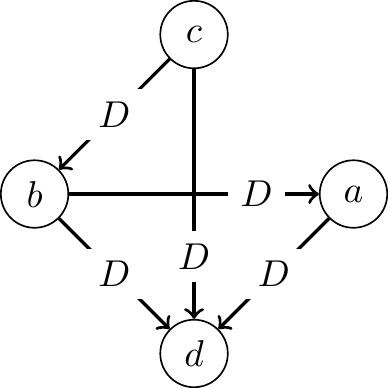
Since \(c\) is not defeated by any other candidate (no arrows labeled with \(D\) point to \(c\)), \(c\) is the unique Split Cycle winner.