19 Elections

An election involves a group of individuals, commonly referred to as voters, who must make a collective decision regarding a set of alternatives, typically known as candidates. The form of this collective decision can vary. It might result in a single winner, a tie among several candidates, a ranking of all candidates, the selection of a committee, or some other outcome.

For the purposes of this course, unless stated otherwise, we will concentrate on single-winner elections. So, the group decision is either a single winner or a set of candidates that are tied for the win. Examples of such elections range from large-scale political events, like the election of a president, to smaller-scale decisions, such as choosing the president of a club or a group of friends deciding where to have dinner.

19.1 Ranked Ballots

In an election, each voter submits a ballot that is meant to express their preferences among the candidates.

In a ranked ballot, voters are asked to rank the candidates in order of preference. Below is an example of a ranked ballot used in the 2019 election for the Mayor of San Francisco:

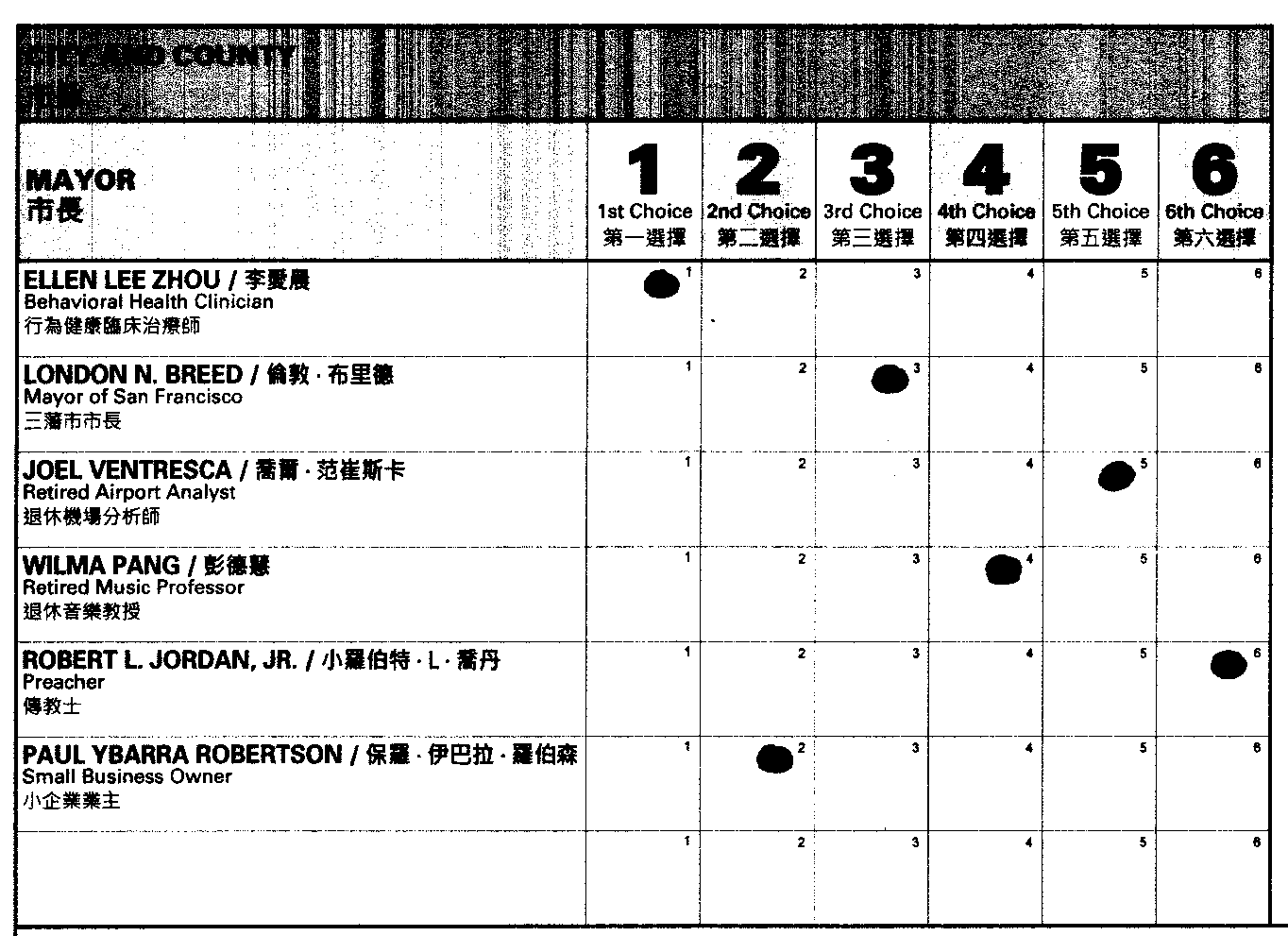
Sample Ballot - 2019 Mayoral Eleciton San Francisco

The ranking provided by the voter can be described as a linear order over the set of candidates. A linear order is a relation $P$ that is asymmetric and transitive over the set of candidates, $\{Zhou, Breed, Ventresca, Pang, Jordan, Robertson\}$. In the case of the above ballot, the linear order is:

\[Zhou \mathrel{P} Robertson \mathrel{P} Breed \mathrel{P} Pang \mathrel{P}Ventresca\mathrel{P}Jordan.\]

In this formalization, $Zhou \mathrel{P} Robertson$ indicates that the voter ranked $Zhou$ over $Robertson$. This is visible on the ballot, as $Zhou$ is marked as the “1st Choice” and $Robertson$ as the “2nd Choice.” Similarly, we have that $Zhou \mathrel{P} Breed$ since $Zhou$ was marked “1st Choice” while $Breed$ was marked “3rd Choice”.

We will often display this ranking of the candidates by listing the candidates from top to bottom in the order of the voter’s preference. For example, the above ranking can be displayed as:

\[\begin{array}{c} Zhou\\ Robertson\\ Breed\\ Pang\\ Ventresca\\ Jordan \end{array}\]

In this course, we will primarily focus on ranked ballots and the various methods used to determine the winner(s) when voters submit ranked ballots. To conclude this section, it is important to clarify the terminology used when discussing voters’ rankings. Consider the following example of two voters, Voter 1 and Voter 2, who have different rankings of the candidates (with $Zhou$ and $Ventresca$ highlighted):

\[\begin{array}{cc} Voter 1 & Voter 2\\\hline \cellcolor{blue}{\textcolor{white}{Zhou}} & Pang\\ Robertson & Breed\\ Breed & \cellcolor{blue}{\textcolor{white}{Zhou}}\\ Pang & \cellcolor{red}{\textcolor{white}{Ventresca}}\\ \cellcolor{red}{\textcolor{white}{Ventresca}} & Jordan\\ Jordan & Robertson \end{array}\]

There are two ways to describe the rankings of $Zhou$ and $Ventresca$ by these voters:

Voter 1 and Voter 2 rank $Zhou$ and $Ventresca$ the same way: Both voters rank $Zhou$ above $Ventresca$.
Voter 1 and Voter 2 rank $Zhou$ and $Ventresca$ in different positions: Voter 1 ranks $Zhou$ in 1st place, while Voter 2 ranks $Zhou$ in 3rd place. Voter 1 ranks $Ventresca$ in 5th place, while Voter 2 ranks $Ventresca$ in 4th place.

Note

In many real-world elections, voters are not required to rank all candidates, and they may even rank two candidates equally, indicating a tie between them. However, for simplicity, we will focus on elections where voters rank all candidates and do not allow ties.

19.2 (Anonymous) Profiles

Suppose that $V$ is the set of voters and $X$ is the set of candidates. Let $L(X)$ denote the set of all rankings over $X$, i.e., the set of all linear orders on $X$. A profile is a description of an election that describes the (ranked) ballot submitted by each voter.

Definition 19.1 (Profile) A profile for the pair $(V, X)$ is a function $\mathbf{P}: V \to L(X)$, which assigns to each voter $i \in V$ a ranking $\mathbf{P}(i) \in L(X)$. We denote the ranking of voter $i$ in profile $\mathbf{P}$ by $\mathbf{P}_i$, and we use $a \mathrel{\mathbf{P}_i} b$ to indicate that voter $i$ ranks candidate $a$ above candidate $b$ in profile $\mathbf{P}$.

For example, suppose that $V = \{v_1, v_2, v_3, v_4, v_5\}$ and $X = \{a, b, c, d\}$. Let $\mathbf{P}$ be a profile for the pair $(V, X)$, depicted in the following table:

\[\begin{array}{ccccc} v_1 & v_2 & v_3 & v_4 & v_5\\\hline a & c & c & a & a\\ b & d & d & b & b\\ c & a & a & c & d\\ d & b & b & d & c\\ \end{array}\]

We note the following about the rankings in profile $\mathbf{P}$:

$v_1$ and $v_4$ submitted the same ranking: $a$ is ranked first, followed by $b$, then $c$, and finally $d.$
$v_2$ and $v_3$ submitted the same ranking: $c$ is ranked first, followed by $d$, then $a$, and finally $b.$
$v_1$, $v_4$, and $v_5$ all rank $a$ above $c.$ That is, $a \mathrel{\mathbf{P}{v_1}} c$, $a \mathrel{\mathbf{P}{v_4}} c$, and $a \mathrel{\mathbf{P}_{v_5}} c.$
$v_2$ and $v_3$ both rank $c$ above $a.$ That is, $c \mathrel{\mathbf{P}{v_2}} a$ and $c \mathrel{\mathbf{P}{v_3}} a.$
all voters rank $a$ above $b$. That is, for all $i\in V$, $a \mathrel{\mathbf{P}_i} b.$

In most elections, we are primarily concerned with how many voters submitted a particular ranking, rather than the identities of the voters who submitted it. When we only list the number of voters associated with each ranking, we refer to this as an anonymous profile. For example, the profile $\mathbf{P}$ above can be represented as an anonymous profile as follows:

\[\begin{array}{ccc} 2 & 2 & 1\\\hline a & c & a\\ b & d & b\\ c & a & d\\ d & b & c\\ \end{array}\]

19.3 Margin of Victory

Given an (anonymous) profile $\mathbf{P}$, we are interested in evaluating how well the candidates performed in the election. One straightforward way to measure the performance of a candidate is by counting how many voters rank that candidate in first place.

For example, consider the following anonymous profile for three candidates $\{a, b, c\}$:

\[\begin{array}{ccc} 34 & 33 & 33\\\hline a & b & c\\ b & c & b\\ c & a & a\\ \end{array}\]

From this profile:

$34$ voters rank $a$ in first place.
$33$ voters rank $b$ in first place.
$33$ voters rank $c$ in first place.

According to this measure, $a$ performed the best, with 34 voters placing $a$ first. However, this measure overlooks an important fact: a significant majority of voters (66) rank $a$ last!

If $a$ did not perform the “best” in this election, we are left with candidates $b$ and $c$. Both candidates received $33$ first-place rankings, resulting in a tie for first place. However, notice that $67$ voters ($34 + 33$) rank $b$ above $c$, while only $33$ voters rank $c$ above $b. Therefore, focusing on the voters’ preferences between $b$ and $c$, $b$ is the clear winner.

Generalizing this idea, for each pair of candidates, we can calculate the margin of victory, which indicates how many more voters rank one candidate above the other.

Definition 19.2 (Margin) Suppose that $V$ is a set of voters and $X$ is a set of candidates, and that $\mathbf{P}$ is a profile for the pair $(V, X)$. For candidates $x, y \in X$, the margin of $x$ over $y$ is the number of voters in $\mathbf{P}$ who rank $x$ above $y$, minus the number of voters who rank $y$ above $x$. We write $Margin_\mathbf{P}(x, y)$ for the margin of $x$ over $y$ in $\mathbf{P}$. Formally, the margin of $x$ over $y$ is given by: \[Margin_\mathbf{P}(x, y) = |\{i\mid x\mathrel{\mathbf{P}_i} y\}| - |\{i\mid y\mathrel{\mathbf{P}_i} x\}|.\]

In the above profile $\mathbf{P}$, we have the following margins:

\[\begin{array}{rclcl} Margin_\mathbf{P}(a, b) & = & 34 - 66 & = & -32\\ Margin_\mathbf{P}(b, a) & = & 66 - 34 & = & 32\\[4pt] Margin_\mathbf{P}(a, c) & = & 34 - 66 & = & -32\\ Margin_\mathbf{P}(c, a) & = & 66 - 34 & = & 32\\[4pt] Margin_\mathbf{P}(b, c) & = & 67 - 33 & = & 34\\ Margin_\mathbf{P}(c, b) & = & 33 - 67 & = & -34\\ \end{array}\]

Note that for any pair of candidates $x$ and $y$, we have: \[Margin_\mathbf{P}(x, y) = -Margin_\mathbf{P}(y, x).\] Additionally, the margin of a candidate over themselves is always zero: \[Margin_\mathbf{P}(x, x) = 0.\]

The margin of victory is a valuable tool for comparing the performance of candidates in an election. In particular, we say that $x$ is majority preferred to $y$ when more voters rank $x$ above $y$ than the other way around.

Definition 19.3 (Majority Preference) Suppose that $V$ is a set of voters and $X$ is a set of candidates, and that $\mathbf{P}$ is a profile for the pair $(V, X)$. For candidates $x, y \in X$, we say that $x$ is majority preferred to $y$ when $Margin_\mathbf{P}(x, y) > 0$.

In the above profile $\mathbf{P}$, we have the following:

$b$ is majority preferred to $a$;
$b$ is majority preferred to $c$; and
$c$ is majority preferred to $a$.

19.4 Margin Graph

Similar to how we visualize relations (see Chapter 2), we can visualize the margins of victory between candidates in a profile $\mathbf{P}$ by listing all the candidates and drawing an edge from candidate $x$ to candidate $y$, labeled with the margin of $x$ over $y$, if $x$ is majority preferred to $y$. This visualization is called the margin graph of the profile $\mathbf{P}$.

The margin graph for the following profile $\mathbf{P}$ \[\begin{array}{ccc} 34 & 33 & 33\\\hline a & b & c\\ b & c & b\\ c & a & a\\ \end{array}\]

is shown below:

We conclude this section with a few observations about the margin graph:

The arrows in a margin graph indicate that candidate $x$ is majority preferred to candidate $y$ when there is an edge from $x$ pointing to $y$. Since $x$ being majority preferred to $y$ implies that $y$ is not majority preferred to $x$, there can be at most one edge between any two candidates in the margin graph.
If there is an even number of voters, there may be a tie between two candidates $x$ and $y$, where $Margin_\mathbf{P}(x, y) = 0$. In this case, no edge will appear between $x$ and $y$ in the margin graph.
If there is an odd number of voters, then there must be a majority preference between any two candidates. In this case, the margin graph will contain an edge between every pair of candidates.

19.5 Exercises

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{ccc} 12 & 8 & 10\\\hline a & b & c\\ c & c & b\\ b & a & a \end{array}\]

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{cccccc} 2 & 2 & 5 & 1 & 4 & 3\\\hline d & b & d & c & c & b\\ c & a & c & b & a & d\\ b & d & a & a & d & a\\ a & c & b & d & b & c \end{array}\]

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{cccccc} 6 & 3 & 4 & 5 & 5 & 1\\\hline d & b & b & d & c & c\\ c & a & d & c & b & a\\ b & d & c & a & a & d\\ a & c & a & b & d & b \end{array}\]

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{cccccc} 4 & 3 & 4 & 2 & 3 & 2\\\hline b & d & c & c & b & a\\ a & c & b & a & d & c\\ d & a & a & d & a & d\\ c & b & d & b & c & b \end{array}\]

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{ccc} 13 & 7 & 6\\\hline a & b & c\\ c & c & b\\ b & a & a \end{array}\]

Solutions

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{ccc} 12 & 8 & 10\\\hline a & b & c\\ c & c & b\\ b & a & a \end{array}\]

The margin of $a$ over $b$ is $12 - 18 = -6$
The margin of $b$ over $a$ is $18 - 12 = 6$
The margin of $a$ over $c$ is $12 - 18 = -6$
The margin of $c$ over $a$ is $18 - 12 = 6$
The margin of $b$ over $c$ is $8 - 22 = -14$
The margin of $c$ over $b$ is $22 - 8 = 14$

The margin graph is:

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{cccccc} 2 & 2 & 5 & 1 & 4 & 3\\\hline d & b & d & c & c & b\\ c & a & c & b & a & d\\ b & d & a & a & d & a\\ a & c & b & d & b & c \end{array}\]

The margin of $a$ over $b$ is $9 - 8 = 1$
The margin of $b$ over $a$ is $8 - 9 = -1$
The margin of $a$ over $c$ is $5 - 12 = -7$
The margin of $c$ over $a$ is $12 - 5 = 7$
The margin of $a$ over $d$ is $7 - 10 = -3$
The margin of $d$ over $a$ is $10 - 7 = 3$
The margin of $b$ over $c$ is $5 - 12 = -7$
The margin of $c$ over $b$ is $12 - 5 = 7$
The margin of $b$ over $d$ is $6 - 11 = -5$
The margin of $d$ over $b$ is $11 - 6 = 5$
The margin of $c$ over $d$ is $5 - 12 = -7$
The margin of $d$ over $c$ is $12 - 5 = 7$

The margin graph is:

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{cccccc} 6 & 3 & 4 & 5 & 5 & 1\\\hline d & b & b & d & c & c\\ c & a & d & c & b & a\\ b & d & c & a & a & d\\ a & c & a & b & d & b \end{array}\]

The margin of $a$ over $b$ is $6 - 18 = -12$
The margin of $b$ over $a$ is $18 - 6 = 12$
The margin of $a$ over $c$ is $3 - 21 = -18$
The margin of $c$ over $a$ is $21 - 3 = 18$
The margin of $a$ over $d$ is $9 - 15 = -6$
The margin of $d$ over $a$ is $15 - 9 = 6$
The margin of $b$ over $c$ is $7 - 17 = -10$
The margin of $c$ over $b$ is $17 - 7 = 10$
The margin of $b$ over $d$ is $12 - 12 = 0$
The margin of $d$ over $b$ is $12 - 12 = 0$
The margin of $c$ over $d$ is $6 - 18 = -12$
The margin of $d$ over $c$ is $18 - 6 = 12$

The margin graph is:

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{cccccc} 4 & 3 & 4 & 2 & 3 & 2\\\hline b & d & c & c & b & a\\ a & c & b & a & d & c\\ d & a & a & d & a & d\\ c & b & d & b & c & b \end{array}\]

The margin of $a$ over $b$ is $7 - 11 = -4$
The margin of $b$ over $a$ is $11 - 7 = 4$
The margin of $a$ over $c$ is $9 - 9 = 0$
The margin of $c$ over $a$ is $9 - 9 = 0$
The margin of $a$ over $d$ is $12 - 6 = 6$
The margin of $d$ over $a$ is $6 - 12 = -6$
The margin of $b$ over $c$ is $7 - 11 = -4$
The margin of $c$ over $b$ is $11 - 7 = 4$
The margin of $b$ over $d$ is $11 - 7 = 4$
The margin of $d$ over $b$ is $7 - 11 = -4$
The margin of $c$ over $d$ is $8 - 10 = -2$
The margin of $d$ over $c$ is $10 - 8 = 2$

The margin graph is:

In the following profile, find the margins of each pair of candidates and draw the margin graph.

\[\begin{array}{ccc} 13 & 7 & 6\\\hline a & b & c\\ c & c & b\\ b & a & a \end{array}\]

The margin of $a$ over $b$ is $13 - 13 = 0$
The margin of $b$ over $a$ is $13 - 13 = 0$
The margin of $a$ over $c$ is $13 - 13 = 0$
The margin of $c$ over $a$ is $13 - 13 = 0$
The margin of $b$ over $c$ is $7 - 19 = -12$
The margin of $c$ over $b$ is $19 - 7 = 12$

The margin graph is: