29 Condorcet Paradox
Consider the following profile \(\mathbf{P}\) (discussed in the previous section):
\[\begin{array}{ccc} 40 & 45 & 15\\\hline b & a & c\\ c & c & b\\ a & b & a \end{array}\]In this profile, candidate \(c\) is majority preferred to \(a\) because \(Margin_\mathbf{P}(c, a) = 10 > 0\), and \(c\) is also majority preferred to \(b\) because \(Margin_\mathbf{P}(c, b) = 20 > 0\). Thus, in head-to-head contests, \(c\) defeats both \(a\) and \(b\). Based on this, it seems clear that \(c\) should be the winner of this election. Interestingly, however, the Plurality voting method would elect candidate \(a\), while Instant Runoff Voting would elect candidate \(b\).
Candidates that are majority preferred to all other candidates are called Condorcet winners.
Definition 29.1 (Condorcet Winner) Suppose that \(V\) is a set of voters and \(X\) is a set of candidates, and that \(\mathbf{P}\) is a profile for the pair \((V, X)\). A candidate \(x\in X\) is called the Condorcet winner provided that for all candidate \(y\in X\), if \(x\neq y\), then \(Margin_\mathbf{P}(x, y) > 0\).
In the profile \(\mathbf{P}\) above, candidate \(c\) is the Condorcet winner. From the perspective of majority preference, \(c\) seems to be the clear winner in this election, while candidate \(a\) (the winner under Plurality) is the obvious loser: Candidate \(a\) is defeated by both \(b\) and \(c\) in head-to-head contests, with \(Margin_\mathbf{P}(b, a) = Margin_\mathbf{P}(c, a) = 10\). A candidate who loses to every other candidate in head-to-head comparisons is referred to as the Condorcet loser.
Definition 29.2 (Condorcet Loser) Suppose that \(V\) is a set of voters and \(X\) is a set of candidates, and that \(\mathbf{P}\) is a profile for the pair \((V, X)\). A candidate \(x\in X\) is called the Condorcet loser provided that for all candidate \(y\in X\), if \(x\neq y\), then \(Margin_\mathbf{P}(y, x) > 0\).
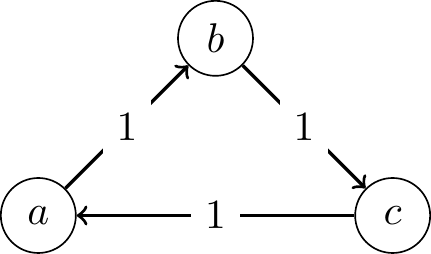
Why not always elect the Condorcet winner? The problem, known as the Condorcet Paradox, is that a Condorcet winner does not always exist. This occurs when every candidate is defeated by at least one other candidate in a head-to-head contest. The following profile demonstrates the Condorcet Paradox:
\[\begin{array}{ccc} 1 & 1 & 1\\\hline a & b & c\\ b & c & a\\ c & a & b \end{array}\]In this profile we have that:
- \(a\) is majority preferred to \(b\) since \(Margin_\mathbf{P}(a, b) = 2-1=1 > 0\).
- \(b\) is majority preferred to \(c\) since \(Margin_\mathbf{P}(b, c) = 2-1=1 > 0\).
- \(c\) is majority preferred to \(a\) since \(Margin_\mathbf{P}(c, a) = 2-1=1> 0\).
Thus, this profile has no Condorcet winner, as \(a\) loses to \(c\), \(b\) loses to \(a\), and \(c\) loses to \(b\) in their respective head-to-head comparisons.
The profile above also illustrates that the majority preference relation may not be transitive. In this profile, \(a\) is majority preferred to \(b\), \(b\) is majority preferred to \(c\), and \(c\) is majority preferred to \(a\), creating a violation of transitivity. In other words, there is a cycle in the majority preference relation, as shown in the margin graph for this profile:
A majority cycle in a profile is a cycle in the majority preference relation.
Definition 29.3 (Majority Cycle) Suppose that \(V\) is a set of voters and \(X\) is a set of candidates, and that \(\mathbf{P}\) is a profile for the pair \((V, X)\). A sequence of candidates \(a_1, \ldots, a_n\) forms a majority cycle when \(a_1\) is majority preferred to \(a_2\), \(a_2\) is majority preferred to \(a_3\), \(\ldots\), \(a_{n-1}\) is majority preferred to \(a_n\), and \(a_n\) is majority preferred to \(a_1\).
When a majority cycle exists in a profile, it indicates that the group of voters has an incoherent preference over a subset of candidates. However, this does not mean that the voters are incoherent about all the candidates. In fact, a Condorcet winner can still exist, even if a majority cycle is present in the profile. Consider the following profile and margin graph:
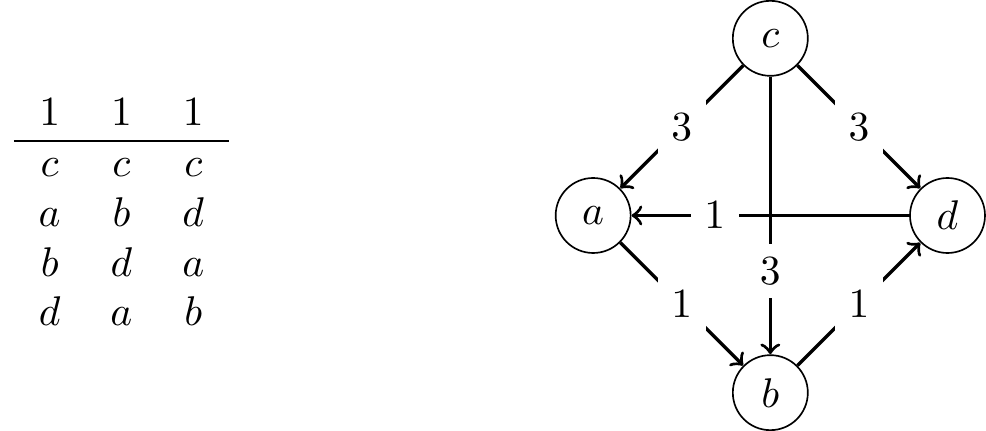
Candidate \(c\) is the Condorcet winner in this profile, as \(c\) is majority preferred to all other candidates. However, a majority cycle exists among the remaining candidates: \(a\) is majority preferred to \(b\), \(b\) is majority preferred to \(d\), and \(d\) is majority preferred to \(a\).