36 Voting Axioms
In the previous chapters, we focused on situations with exactly two alternatives, where May’s Theorem (Chapter 33) showed Majority Rule to be the uniquely fair voting method. Indeed, when there are only two alternatives, all reasonable voting methods reduce to Majority Rule.
However, when there are more than two alternatives, the situation becomes more complex. There is no single “best” voting method - instead, there are many reasonable ways to extend Majority Rule, each with its own advantages and drawbacks (see Chapter 31).
This raises a fundamental question: How should we evaluate different voting methods? One approach is to identify principles, or axioms, that capture desirable features of group decision-making. This chapter examines several key axioms and explores how different voting methods satisfy or fail them.
36.1 Anonymity and Neutrality
The two most basic fairness axioms are Anonymity and Neutrality, which we encountered in our discussion of May’s Theorem (Section 33.1). We restate these axioms here for convenience.
Definition 36.1 (Anonymity) A voting method \(F\) satisfies anonymity if rearranging the voters’ ballots in any way does not change the set of winners. In other words, if \(\mathbf{P}\) is a profile and \(\mathbf{P}'\) is another profile that is exactly like \(\mathbf{P}\) except that some of the voters have swapped their ballots, then \(F(\mathbf{P})=F(\mathbf{P}')\).
Definition 36.2 (Neutrality) A voting method \(F\) satisfies neutrality if swapping the candidates in all the voters ballots leads to an equivalent swap in winners. More precisely:
- Given any profile \(\mathbf{P}\),
- Create a new profile \(\mathbf{P}'\) by swapping \(a\) and \(b\) in every voter’s ballot,
- Then \(F(\mathbf{P}')\) must be the same as \(F(\mathbf{P})\) with \(a\) and \(b\) swapped.
Any sensible voting method should treat all voters equally and all candidates equally. Indeed, all of the voting methods we have studied satisfy both of these basic fairness axioms.
These fairness axioms lead to an important impossibility result: no voting method can simultaneously satisfy both Anonymity and Neutrality while always selecting a single winner. To state this precisely, we first define what it means for a voting method to always select a single winner:
Definition 36.3 (Resoluteness) A voting method \(F\) satisfies resoluteness if for any profile \(\mathbf{P}\), \(F(\mathbf{P})\) is a singleton set. In other words, \(F\) always selects a single winner.
This leads us to the following important result:
Theorem 36.1 There is no voting method \(F\) that satisfies Anonymity, Neutrality, and Resoluteness.
36.2 Dominance Axioms
The axioms in this section capture the idea that if one candidate should clearly be the winner, then that candidate should win, or if a candidate should clearly not be the winner, then that candidate should lose. The most basic of these is the Pareto principle:
Definition 36.4 (Pareto) A voting method \(F\) satisfies the Pareto principle, also called the Unanimity principle, if for any profile \(\mathbf{P}\), whenever every voter ranks candidate \(x\) above candidate \(y\), then \(y\) cannot be a winner. That is, in a profile \(\mathbf{P}\), if for all voters \(i\) we have that \(x\mathrel{\mathbf{P}_i} y\), then \(y\notin F(\mathbf{P})\).
The Pareto principle is uncontroversial - if everyone prefers \(x\) to \(y\), then \(y\) should not win. Indeed, all standard voting methods satisfy this basic requirement.
Two stronger principles involve the concept of Condorcet winners and losers. Recall that in a profile \(\mathbf{P}\):
- A Condorcet winner is a candidate who defeats every other candidate in pairwise majority comparisons. More precisely, a candidate \(x\) is a Condorcet winner if \(Margin_\mathbf{P}(x, y) > 0\) for all candidates \(y \neq x\).
- A Condorcet loser is a candidate who is defeated by every other candidate in pairwise majority comparisons. More precisely, a candidate \(x\) is a Condorcet loser if \(Margin_\mathbf{P}(x, y) < 0\) for all candidates \(y \neq x\).
These concepts lead to two important principles:
Definition 36.5 (Condorcet Principles)
- A voting method \(F\) satisfies the Condorcet winner principle if whenever a candidate \(x\) is a Condorcet winner, then \(x\) must be the unique winner. That is, in a profile \(\mathbf{P}\), if \(x\) is a Condorcet winner in \(\mathbf{P}\), then \(F(\mathbf{P}) = \{x\}\).
- A voting method \(F\) satisfies the Condorcet loser principle if whenever a candidate \(x\) is a Condorcet loser, then \(x\) cannot be a winner. That is, in a profile \(\mathbf{P}\), if \(x\) is a Condorcet loser in \(\mathbf{P}\), then \(x\notin F(\mathbf{P})\).
Plurality voting provides a striking example of how both Condorcet principles can be violated. Consider the following profile and its corresponding margin graph:
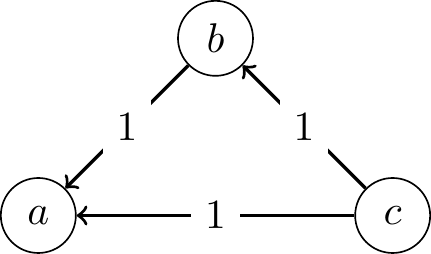
In this profile, \(a\) is the unique Plurality winner with 3 first-place votes (compared to 2 each for \(b\) and \(c\)). However, examining the pairwise comparisons reveals two problems:
- \(a\) is actually the Condorcet loser, losing both pairwise comparisons: more voters prefer \(b\) to \(a\) and more voters prefer \(c\) to \(a\).
- \(c\) is the Condorcet winner, defeating both \(a\) and \(b\) in pairwise comparisons. Yet Plurality fails to select \(c\) as the unique winner.
This single example demonstrates that Plurality violates both Condorcet principles: it can elect a Condorcet loser and fail to elect a Condorcet winner.
36.3 Monotonicity
A basic intuition about voting is that increased support for a candidate should never hurt that candidate’s chances of winning. If some voters move a candidate higher in their rankings while all other voters’ preferences remain unchanged, that candidate should not go from being a winner to being a loser. This intuition is captured by the monotonicity axiom:
Definition 36.6 (Monotonicity) A voting method \(F\) satisfies monotonicity if for any profile \(\mathbf{P}\) where candidate \(x\) is a winner (i.e., \(x\in F(\mathbf{P})\)), and any profile \(\mathbf{P}'\) obtained from \(\mathbf{P}\) by one voter moving \(x\) higher in their ranking (with all other rankings unchanged), then \(x\) must still be a winner in \(\mathbf{P}'\) (i.e., \(x\in F(\mathbf{P}')\)).
Surprisingly, some common voting methods violate this seemingly basic requirement. This leads to what Fishburn and Brams (1983) call the More-is-Less Paradox: a candidate can win an election but then lose if they receive additional support, all else remaining equal. Instant Runoff Voting (aka Ranked Choice Voting) provides a striking example of this paradox. Consider the following two profiles \(\mathbf{P}\) and \(\mathbf{P}'\), each with 17 voters:
Consider how Instant Runoff Voting works in these two profiles:
- In profile \(\mathbf{P}\), \(a\) is the Instant Runoff Voting winner:
- First round:
- 6 voters rank \(a\) in first-place.
- 6 voters rank \(b\) in first-place.
- 5 voters rank \(c\) in first-place.
- Final round:
- 11 voters rank \(a\) in first-place (6 original + 5 from \(c\) voters).
- 6 voters rank \(b\) in first-place.
- First round:
- In profile \(\mathbf{P}'\), \(b\) is the Instant Runoff Voting winner:
- First round:
- 8 voters rank \(a\) in first-place.
- 4 voters rank \(b\) in first-place.
- 5 voters rank \(c\) in first-place.
- Final round:
- 8 voters rank \(a\) in first-place.
- 9 voters rank \(c\) in first-place (5 original + 4 from \(b\) voters).
- First round:
This demonstrates a violation of monotonicity: by gaining more support (two voters moving \(a\) to first place), candidate \(a\) goes from winning to losing. Other methods like Plurality, Borda Count, and Copeland satisfy monotonicity.
There’s another way to think about a candidate receiving “more support.” Instead of existing voters ranking a candidate higher (as in Definition 36.6), new voters might show up who rank that candidate first. This leads to another intuitive principle called positive involvement:
Definition 36.7 (Positive Involvement) A voting method satisfies positive involvement if whenever candidate \(a\) would win had a group of voters not participated, and all voters in this group rank \(a\) first, then \(a\) must still win when these voters do participate.
In other words, if a candidate would win without certain voters participating, and those voters all strongly support that candidate, their participation should not cause that candidate to lose. Surprisingly, some standard voting methods violate this seemingly basic requirement. Below, we will see examples of how Copeland and Coombs violate Positive Involvement.
The Coombs voting method violates Positive Involvement. Consider the following profile:
\[\begin{array}{ccccccc} 2 & 2 & 1 & 1 & 2 & 1 & 1 \\\hline c & b & d & d & c & a & b \\ a & a & c & a & b & d & d \\ b & c & b & c & d & b & a \\ d & d & a & b & a & c & c \\ \end{array}\]In this profile, the unique Coombs winner is \(b\) (the order of elimination is first \(d\) is removed, then \(c\) is removed). Now suppose a new voter arrives who ranks \(b\) first (\(b\ d\ c\ a\)). With this additional voter:
\[\begin{array}{cccccccc} 2 & 2 & 1 & 1 & 2 & 1 & 1 & 1 \\\hline c & b & d & d & c & a & b & \cellcolor[gray]{.8}{b} \\ a & a & c & a & b & d & d & \cellcolor[gray]{.8}{d} \\ b & c & b & c & d & b & a & \cellcolor[gray]{.8}{c} \\ d & d & a & b & a & c & c & \cellcolor[gray]{.8}{a} \\ \end{array}\]In this new profile, \(a\) and \(c\) are tied for the most last place votes, and so both are eliminated, resulting in \(c\) being the unique Coombs winner.
This violates Positive Involvement: even though \(b\) was winning, and a new voter who ranks \(b\) first joined the election, \(b\) lost! The paradox occurs because the new ballot changes the elimination order in early rounds, leading to a completely different outcome.
Now, we show that the Copeland voting method violates Positive Involvement. Consider the following profile with the majority graph next to it:
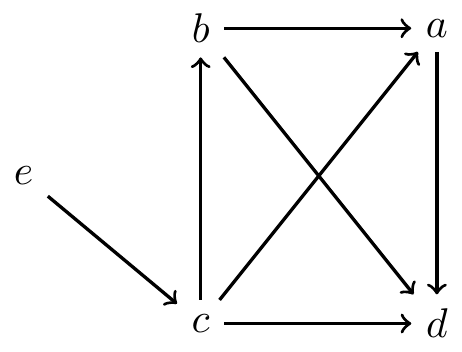
The Copeland winner is \(c\) since it has the largest win-loss record of \(2\). Now suppose a new voter arrives who ranks \(c\) first (\(c\ e\ d\ b\ a\)). With this additional voter:
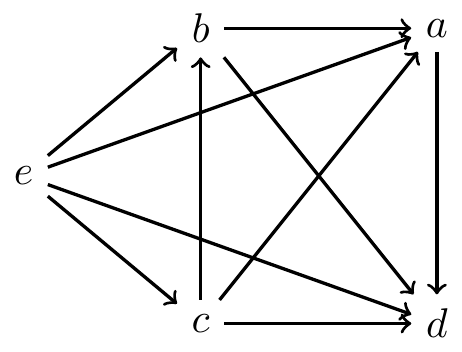
Since \(e\) is now the Condorcet winner, \(e\) is the unique Copeland winner.
This violates Positive Involvement: even though \(c\) was winning, and a new voter who ranks \(c\) first joined the election, \(c\) lost!
36.4 Spoilers
A persistent criticism of many voting methods is the “spoiler effect” - where adding a new candidate can cause an apparently irrational change in the winner. As one organizer noted in a 2004 letter to the Washington Post, “Why is it that we can put a man on the moon but can’t come up with a way to elect our president that allows voters to vote for their favorite candidate, allows multiple candidates to run… and makes the ‘spoiler’ problem go away?”
The most famous example is from the 2000 U.S. Presidential election in Florida:
\[\begin{array}{ccc} 2,912,790 & 2,912,253 & 97,488 \\\hline Bush & \cellcolor{gray!30}{Gore} & \cellcolor{gray!30}{Nader} \\ \cellcolor{gray!30}{Gore} & \cellcolor{gray!30}{Nader} & \cellcolor{gray!30}{Gore} \\ \cellcolor{gray!30}{Nader} & Bush & Bush \end{array}\]In this case, Nader “spoiled” the election for Gore. Without Nader in the race, Gore would have won Florida (and thus the presidency). A clear majority of voters preferred Gore to Nader, yet Nader’s presence caused both Gore and Nader to lose to Bush.
Similar problems can occur with other voting methods. Consider this example from the 2009 Burlington mayoral election using Instant Runoff Voting (the following example is taken from www.electionscience.org/library/the-spoiler-effect/, “a simplified approximation of what happened in the 2009 IRV mayoral election in Burlington, Vermont.”):
\[\begin{array}{ccc} 37 & 29 & 34 \\\hline r & d & p \\ d & p & d \\ p & r & r \end{array}\]In this profile, the Democrat would win without the Republican in the race. However, with the Republican included, the Progressive wins - even though a majority preferred the Democrat to the Republican.
This leads to a natural property we might want voting methods to satisfy:
Definition 36.8 (Immunity to Spoilers) A voting method satisfies immunity to spoilers if the following cannot happen:
- Candidate \(a\) would win without candidate \(b\) in the election
- A majority of voters prefer \(a\) to \(b\)
- But with \(b\) in the election, both \(a\) and \(b\) lose
This criterion would rule out all the problematic spoiler effects discussed in this section. Surprisingly, among standard voting methods, only Minimax, Copeland, and Split Cycle satisfy this property. Other methods, including Plurality and Instant Runoff Voting as we have seen, but also Borda, violate this property.
To see that Borda Count also violates Immunity to Spoilers, consider this profile \(\mathbf{P}\):
\[\begin{array}{cc} 2 & 3 \\\hline c & a \\ b & c \\ a & b \\ \end{array}\]Without candidate \(b\) in the election, the profile would be:
\[\begin{array}{cc} 2 & 3 \\\hline c & a \\ a & c \\ \end{array}\]Here, \(a\) is the Borda winner (scoring 3 points to \(c\)’s 2 points)
In the original profile \(\mathbf{P}\):
- A majority prefers \(a\) to \(b\) (3 voters versus 2).
- Yet \(c\) is the Borda winner, with both \(a\) and \(b\) losing.
36.5 Multiple-Districts
Suppose that an election is conducted across multiple districts, and each district elects a winner. We might expect that if a candidate wins in every district, they should win the overall election when the districts are combined. This intuition is captured by the following axiom:
Definition 36.9 (Multiple Districts Property) If a candidate wins in each district individually, then that candidate should also win when all the districts are merged.
Some voting methods do satisfy the Multiple Districts Property in a straightforward way. Consider Plurality voting: if candidate \(a\) has the most first-place votes in each district, they must also have the most first-place votes when the districts are combined. Similarly for Borda: if \(a\) has the highest Borda score in each district, they will have the highest Borda score in the combined election.
However, any Condorcet-consistent voting method must violate this property. To see this, consider the following example of two districts:
| District 1 | District 2 |
| \[\begin{array}{ccc} 2 & 2 & 2\\\hline a & b & c \\ b & c & a \\ c & a & b \end{array}\] | \[\begin{array}{cc} 1 & 2 \\\hline a & b \\ b & a \\ c & c \end{array}\] |
In District 1, due to the cycle in preferences, all candidates tie for winner (assuming anonymity and neutrality). In District 2, \(b\) is the Condorcet winner. Thus, \(b\) wins both districts. However, when we combine the districts, we have the following profile:
\[\begin{array}{ccccc} 2 & 2 & 2 & 1 & 2\\\hline a & b & c & a & b \\ b & c & a & b & a\\ c & a & b & c & c \end{array}\]In this profile, \(a\) is the Condorcet winner. Thus, \(b\) does not win when the two districts are merged! This shows that any Condorcet-consistent method must violate the Multiple Districts Property.
36.5.1 Referendum Paradox
A related phenomenon occurs in referendums conducted across multiple districts. Consider the following example with five districts (\(D_1\) through \(D_5\)), where each row represents one voter’s Yes/No vote about a single issue:
\[\begin{array}{ccccc} D_1 & D_2 & D_3 & D_4 & D_5 \\\hline Y & Y & N & N & N\\ N & Y & Y & N & N \\ Y & N & Y & N & N \\ \end{array}\]This creates a striking paradox:
- Looking at the overall vote totals, “No” wins a majority (9 \(N\) votes compared to 6 \(Y\) votes)
- But looking district by district:
- In \(D_1\): “Yes” wins (2 \(Y\) votes vs 1 \(N\) vote)
- In \(D_2\): “Yes” wins (2 \(Y\) votes vs 1 \(N\) vote)
- In \(D_3\): “Yes” wins (2 \(Y\) votes vs 1 \(N\) vote)
- In \(D_4\) and \(D_5\): “No” wins (all \(N\) votes)
This “referendum paradox” illustrates how electoral systems based on districts or regions can produce outcomes that conflict with the overall majority preference.
36.6 Summary
The table below summarizes which axioms are satisfied by different voting methods:
| Plurality | Borda | Instant Runoff Voting | Coombs | Copeland | Minimax | Split Cycle | |
|---|---|---|---|---|---|---|---|
| Anonymity | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) |
| Neutrality | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) |
| Pareto | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) |
| Condorcet Winner | ✗ | ✗ | ✗ | ✗ | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) |
| Condorcet Loser | ✗ | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | ✗ | \(\checkmark\) |
| Monotonicity | \(\checkmark\) | \(\checkmark\) | ✗ | ✗ | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) |
| Positive Involvement | \(\checkmark\) | \(\checkmark\) | \(\checkmark\) | ✗ | ✗ | \(\checkmark\) | \(\checkmark\) |
| Immunity to Spoilers | ✗ | ✗ | ✗ | ✗ | ✗ | \(\checkmark\) | \(\checkmark\) |
| Multiple Districts | \(\checkmark\) | \(\checkmark\) | ✗ | ✗ | ✗ | ✗ | ✗ |
This table shows there is no “perfect” voting method satisfying all desirable properties. Instead, we face fundamental trade-offs. For instance, we must choose between having a method that is Condorcet-consistent and one that behaves well when combining districts. Understanding these trade-offs is crucial for selecting an appropriate voting method.