9  Background: Lotteries

Suppose that \(X\) is a finite set. A lottery on \(X\) is a function that assigns a probability to each element of \(X\). The elements of \(X\) are called outcomes or prizes.

Definition 9.1 (Lottery) Suppose that \(X\) is a finite set. A lottery, or probability, on \(X\) is a function \(p:X \rightarrow [0, 1]\) such that \(\sum_{x\in X} p(x) = 1\).

Note

This course simplifies some of the mathematical details about probability by assuming that the set \(X\) is finite. This allows us to focus on the key concepts without going into the more complex aspects of probability theory.

To simplify notation, we represent a lottery \(p: X \rightarrow [0, 1]\) on a set \(X = \{x_1, \ldots, x_n\}\) as a linear combination:

\[p(x_1)\cdot x_1 + p(x_2)\cdot x_2 + \cdots + p(x_n)\cdot x_n\]

For instance, if \(X=\{a, b, c\}\), then the following are examples of three lotteries on \(X\):

  1. \(0\cdot a + 1\cdot b + 0\cdot a\): There is a 100% chance of getting \(b\).
  2. \(0.25\cdot a + 0.35 \cdot b + 0.4\cdot c\): There is a 25% chance of getting \(a\), 35% chance of getting \(b\), and a 40% chance of getting \(c\).
  3. \(0.25\cdot a + 0.75\cdot b + 0\cdot c\): There is a 25% chance of getting \(a\) and a 75% chance of getting \(b\).

We will use the following notation for lotteries throughout these notes:

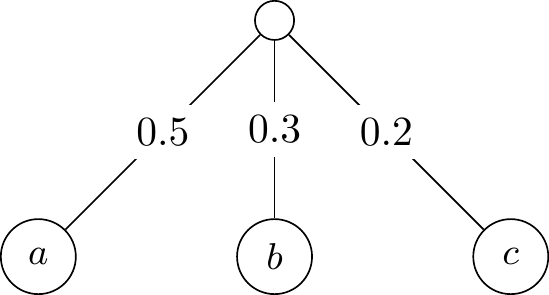
We can represent a lottery \(p_1 \cdot x_1 + \cdots + p_n \cdot x_n\) as a tree, where each edge from the root node leads to an outcome, labeled by its corresponding probability \(p_i\). For example, the lottery \(0.5 \cdot a + 0.3 \cdot b + 0.2 \cdot c\) can be visualized as follows:

In this course, we will often encounter situations where multiple lotteries are combined, leading to what is known as a compound lottery. In a compound lottery, the outcome of one lottery determines which subsequent lottery is played.

For example, suppose \(L_1 = 0.5 \cdot a + 0.5 \cdot b\) and \(L_2 = 0.25 \cdot b + 0.75 \cdot c\) are two lotteries on \(X = {a, b, c}\). Now, imagine a scenario where a fair coin is flipped: if it lands heads, the lottery \(L_1\) is played; if tails, the lottery \(L_2\) is played. This compound lottery is represented as \(0.5 \cdot L_1 + 0.5 \cdot L_2\).

A key point in evaluating such lotteries is that only the final probabilities assigned to each outcome matter. Thus, the compound lottery \(0.5 \cdot L_1 + 0.5 \cdot L_2\) can be simplified as follows:

\[ \begin{eqnarray} 0.5 \cdot L_1 + 0.5\cdot L_2 & = & 0.5\cdot(0.5\cdot a + 0.5 \cdot b) + 0.5\cdot(0.25 \cdot b + 0.75\cdot c) \\ & = & 0.5\times 0.5\cdot a + (0.5\times 0.5 + 0.5 \times 0.25)\cdot b + 0.5\times 0.75\cdot c\\ & = & 0.25\cdot a + 0.375 \cdot b + 0.375\cdot c \end{eqnarray} \]

9.1 Exercises

  1. Consider the lottery in which a fair coin is flipped. If it lands heads, then you win \(\$100\) and if it lands tails, you lose $100. Write this lottery down using the notation described above.

  2. Consider the lottery in which a biased coin is flipped. If it lands heads, then you win \(\$100\) and if it lands tails, you lose $100. Suppose that bias of the coin is that the chance for heads is 3-times the chance for tails. Write this lottery down using the notation described above.

  3. Consider the lottery in which a fair coin is flipped. If it lands heads, then the you lose \(\$5\) and if it lands tails, then you roll a fair die (with 6-sides) and you win the amount in dollars shown on the die. Write this lottery down using the notation described above.

  4. Let \(L_1 = 0.3\cdot \$10: 0.3 + 0.7 \cdot \$5\) and consider the lottery \(0.5\cdot \$10 + 0.5 \cdot L_1\). What is the probability that you will \(\$10\)? What is the probability that you win \(\$5\)?

  1. Consider the lottery in which a fair coin is flipped. If it lands heads, then you win \(\$100\) and if it lands tails, you lose $100. Write this lottery down using the notation described above.

    \[0.5\cdot \$100 + 0.5\cdot -\$100:0.5\]

  2. Consider the lottery in which a biased coin is flipped. If it lands heads, then you win \(\$100\) and if it lands tails, you lose $100. Suppose that bias of the coin is that the chance for heads is 3-times the chance for tails. Write this lottery down using the notation described above.

    \[0.75\cdot \$100 + 0.25 \cdot -\$100:0.25\]

  3. Consider the lottery in which a fair coin is flipped. If it lands heads, then the you lose \(\$5\) and if it lands tails, then you roll a fair die (with 6-sides) and you win the amount in dollars shown on the die. Write this lottery down using the notation described above.

    \[\frac{1}{2} \cdot (-\$5) + \frac{1}{12} \cdot \$1 + \frac{1}{12} \cdot \$2 + \frac{1}{12} \cdot \$3 + \frac{1}{12} \cdot \$4 + \frac{1}{12} \cdot \$5 + \frac{1}{12} \cdot \$6 \]

  4. Let \(L_1 = 0.3\cdot \$10: 0.3 + 0.7 \cdot \$5\) and consider the lottery \(0.5\cdot \$10 + 0.5 \cdot L_1\). What is the probability that you will \(\$10\)? What is the probability that you win \(\$5\)?

    • What is the probability that you will \(\$10\)? \(0.5 + 0.5 * 0.3 = 0.65\)
    • What is the probability that you win \(\$5\)? \(0.5 * 0.7 = 0.35\)