19 Newcomb’s Paradox
Imagine you are standing in front of two boxes:
- Box \(A\), which contains $1,000.
- Box \(B\), which contains either $1,000,000 or nothing.
You can see what is inside Box A, but the contents of Box B are hidden from view:
You are offered two choices:
- one-box: choose only box \(B\)
- two-box: choose both box \(A\) and box \(B\)
You can keep whatever is inside any box that you open, but you will not get to keep what is inside a box that you do not open.
A highly powerful being, known as the Predictor, who has always been very accurate in predicting your behavior, has already acted based on its prediction of your choice:
- If the Predictor has foreseen that you will choose only Box B, it has placed $1,000,000 in Box B.
- If the Predictor has foreseen that you will choose both boxes, it has left Box B empty.
So, which option will you choose: one-box or two-box?
This is known as Newcomb’s Paradox (Nozick 1969). You should answer the above question before reading further.
To formalize the decision problem described above, we can define the components as follows:
- Actions:
- One-box: Selecting only Box \(B\).
- Two-box: Selecting both Box \(A\) and Box \(B\).
- Outcomes:
- \(1M\): You receive 1 million dollars.
- \(1T\): You receive 1 thousand dollars.
- \(0\): You receive nothing.
- \(1M+1T\): You receive one million one thousand dollars.
- States:
- \(pred_B\): The Predictor has predicted that you will choose only Box \(B\).
- \(pred_AB\): The Predictor has predicted that you will choose both Box \(A\) and Box \(B\).
With these components, the decision matrix representing the decision problem is as follows:
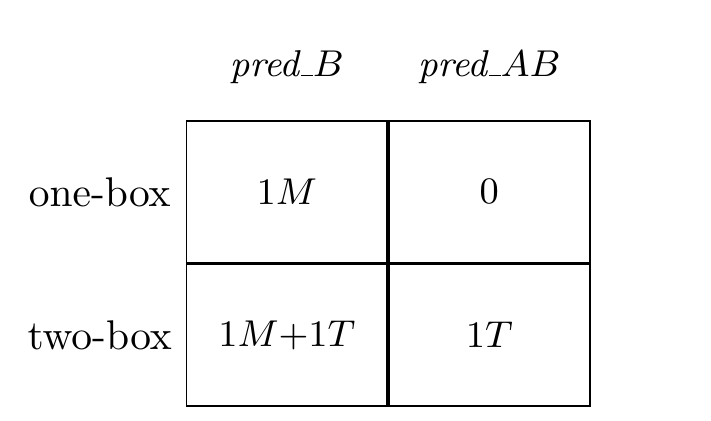
In this decision problem:
- If you choose the one-box action and the Predictor predicted this, you end up with 1 million dollars (\(1M\)).
- If you choose the one-box action but the Predictor predicted that you would choose both, you end up with nothing (\(0\)).
- If you choose the two-box action and the Predictor predicted this, you receive only the 1 thousand dollars from Box A (\(1T\)).
- If you choose the two-box action but the Predictor predicted you would only choose Box B, you receive both the 1 million dollars from Box B and the 1 thousand dollars from Box A (\(1M + 1T\)).
There are two ways to reason about which action you should choose.
Choose Two-Box:
There are two possible states: \(pred\_B\) (the Predictor predicts you will choose only Box \(B\)) and \(pred\_AB\) (the Predictor predicts you will choose both boxes).If the state is \(pred\_B\), then choosing two-box results in the outcome of \(1T\) (you receive \(\$1,000\)), which is strictly better than the one-box outcome of \(\$0\) (you receive nothing).
If the state is \(pred\_AB\), then choosing two-box results in the outcome of \(1M + 1T\) (you receive \(\$1,001,000\)), which is strictly better than the one-box outcome of \(1M\) (you receive \(\$1,000,000\)).
In both states, choosing two-box gives a better outcome than one-box, suggesting that two-box is the rational choice.
Choose One-Box: Let \(B\) denote the event that one-box is chosen and \(AB\) is the event that the action two-box is chosen. To determine the expected utilities of these actions, consider the following conditional probabilities:
- \(P(pred\_B \mid B)\): The probability that the Predictor predicted you would choose only Box \(B\) given that you actually choose Box \(B\).
- \(P(pred\_AB \mid B)\): The probability that the Predictor predicted you would choose both boxes given that you actually choose only Box \(B\).
- \(P(pred\_B \mid AB)\): The probability that the Predictor predicted you would choose only Box \(B\) given that you actually choose both boxes.
- \(P(pred\_AB \mid AB)\): The probability that the Predictor predicted you would choose both boxes given that you actually choose both boxes.
Now, using these probabilities, we can calculate the expected utilities of the actions. Assuming for simplicity that:
- The utility of receiving \(1M\) is \(1,000,000\),
- The utility of receiving \(0\) is \(0\),
- The utility of receiving \(1M + 1T\) is \(1,001,000\),
- The utility of receiving \(1T\) is \(1,000\),
We get the following expected utilities:
- \(EU(\textbf{one-box}) = 1,000,000 \times Pr(pred_B \mid B) + 0 \times Pr(pred_AB \mid B)\)
- \(EU(\textbf{two-box}) = 1,001,000 \times Pr(pred_B \mid AB) + 1,000 \times Pr(pred_AB \mid AB)\)
Since the Predictor is assumed to be very accurate, we have:
- \(P(pred\_B \mid B) \approx 1\) and \(P(pred\_AB \mid AB) \approx 1\), while
- \(P(pred\_AB \mid B) \approx 0\) and \(P(pred\_B \mid AB) \approx 0\).
This implies that the expected utility for choosing one-box is much greater than for two-box:
\[1,000,000 \times P(pred\_B \mid B) + 0 \times P(pred\_AB \mid B)\] is signficantly greater than \[1,001,000 \times P(pred\_B \mid AB) + 1,000 \times P(pred\_AB \mid AB)\]
Therefore, \(EU(\textbf{one-box}) > EU(\textbf{two-box})\), suggesting that one-box should be chosen.
Newcomb’s paradox is interesting because it presents a scenario where maximizing expected utility seems to endorse an action that is strictly dominated. A common response to this paradox is to note that there is an unusual aspect to the expected utility calculations: they assume that the Predictor’s prediction is probabilistically dependent on your choice of action, even though there is no assumption that your choice has any causal influence on the Predictor’s prediction. The crucial point here is that the Predictor made its prediction before you made your decision. For more in-depth discussions of solutions to Newcomb’s paradox, see Collins (1999) and Weirich (2020).
This discussion highlights a fundamental issue with Newcomb’s paradox: it sets up a decision problem where the states are not independent of the actions chosen by the decision maker. In Rational Choice Theory, a standard assumption is to avoid decision problems in which actions and states are interdependent in this manner.
- Act-State Independence
- In any decision problem \((S, O, A)\), if \(P\) is the probability assigned to states, \(X\) is the event that the decision maker chose action \(x\), then for all states \(s\), \(P(s)=P(s\mid X)\). That is, the probability assigned to a state \(s\) is independent of the action chosen by the decision maker.
This assumption helps maintain a clear separation between the decision maker’s choice and the conditions under which those choices are evaluated.
To illustrate this, consider the following representation of a decision problem from Chapter 17 (repeated here for convenience):
- Bet 1: You receive \(\$100\) if it rains tomorrow at noon.
- Bet 2: You receive \(\$200\) if it does not rain tomorrow at noon.
| choose the correct bet | choose the wrong bet | |
| bet 1 | win $100 | receive nothing |
| bet 2 | win $200 | receive nothing |
This representation suggests that bet 2 is clearly better than bet 1 (since bet 2 weakly dominates bet 1). However, the complication arises from the fact that which of the two states is realized depends not only on whether it rains tomorrow at noon but also on the act chosen by the decision maker. This interdependence between the decision maker’s action and the states violates the principle of act-state independence. It complicates the evaluation of the bets because the decision maker’s choice influences the conditions under which the outcomes are determined, thereby undermining the necessary distinction between the actions taken and the resulting outcomes.