2 Background: Relations

The order of elements in a set does not matter. For example, \(\{a, b\}\) is the same set as \(\{b, a\}\) because both denote the set containing the elements \(a\) and \(b\). Similarly, listing the same element more than once does not change the set. So, \(\{a, a, b\}\) is the same set as \(\{a, b\}\).

When the order of elements is important, we use ‘\((\)’ and ‘\()\)’. For example, \((a, b)\) is called an ordered pair, or a tuple of length 2. The first component is \(a\), and the second component is \(b\). Because the order matters, \((a, b)\) is different from \((b, a)\). While there is only one set containing two elements constructed from \(a\) and \(b\), there are four different ordered pairs that can be constructed from \(a\) and \(b\): \[(a, a)\qquad (a, b)\qquad (b, a)\qquad (b, b).\]

Lecture
Slides

Definition 2.1 (Product) Suppose that \(A\) and \(B\) are non-empty sets. The product of \(A\) and \(B\), denoted \(A\times B\), is the set of ordered pairs where the first component comes from \(A\) and the second component comes from \(B\). That is,

\[A\times B=\{(a,b)\ |\ a\in A\text{ and } b\in B\}.\]

Suppose that \(X=\{a, b, c\}\) and \(Y=\{1, 2\}\). Then we have the following:

\(X\times Y=\{(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)\}.\)
\(Y\times X=\{(1,a), (1,b), (1,c), (2,a), (2,b), (2,c)\}.\)
\(X\times X=\{(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)\}.\)

Tuples of length greater than 2

Suppose that \(X=\{a, b\}\) and \(Y=\{d, e\}\), we have that \((X\times X)\times Y\) is \[\{((a,a),d), ((a,b),d), ((b, a),d), ((b,b),d), ((a,a),e), ((a,b),e), ((b, a),e), ((b,b),e)\}.\]

So, elements of \((X\times X) \times Y\) are tuples where the first component is a tuple of length 2 (where each component is from \(X\)) and the second component is an element of \(Y\). Often we will drop the parentheses, writing \(X\times X\times Y\), and view the elements of this set as tuples of length 3:

\[\{(a,a,d), (a,b,d), (b,a,d), (b,b,d), (a,a,e), (a,b,e), (b,a,e), (b,b,e)\}.\]

The parentheses can be recovered by associating them to the left.

Definition 2.2 (Relation) A relation on a set \(X\) is a subset of \(X\times X\) (the set of pairs of elements from \(X\)). That is, if \(R\subseteq X\times X\), then \(R\) is a relation on \(X\).

Relations are a fundamental mathematical tool used throughout Philosophy, Political Science, and Economics. You have already encountered binary relations during your mathematical education: \(=,\le, \ge, <,\) and \(>\) are all examples of relations on numbers, such as the natural numbers \(\mathbb{N}\), real numbers \(\mathbb{R}\), or rational numbers \(\mathbb{Q}\). Similarly, \(\subseteq\) is a relation on the power set of a set.

For instance, the binary relation \(\ge \subseteq \mathbb{N} \times \mathbb{N}\) is the set of all pairs of natural numbers \((a, b)\) where \(a\) is greater than or equal to \(b\): \[\{(a,b)\ |\ a,b\in\mathbb{N}\text{ and } a\text{ is greater than or equal to } b\}.\]

2.1 Notation

Given a set \(R \subseteq X \times X\) of ordered pairs, the expression \((a, b) \in R\) means that \(a\) is related to \(b\) according to \(R\). Conversely, if \((a, b) \notin R\), then \(a\) is not related to \(b\) according to \(R\). To simplify the notation, we write \(a \mathrel{R} b\) when \((a, b) \in R\).

Below is a summary of the notation you will use this semester:

Mathematical Notation	Meaning
\((a, b)\in R\)	\(a\) is related to \(b\) according to \(R\).
\(a\mathrel{R} b\)	\(a\) is related to \(b\) according to \(R\).
\((a, b)\notin R\)	\(a\) is not related to \(b\) according to \(R\).
not-\(a\mathrel{R} b\)	\(a\) is not related to \(b\) according to \(R\).
\(a\mathrel{R\mkern-9.75mu/} b\)	\(a\) is not related to \(b\) according to \(R\).

For instance, we can express that \(4\) is greater-than-or-equal-to \(1\) by writing \(4\geq 1\) or \((4, 1)\in \geq\), and that \(2\) is not greater-than-or-equal-to \(3\) by writing \(2\not\geq 3\) or \((2,3)\notin\geq\).

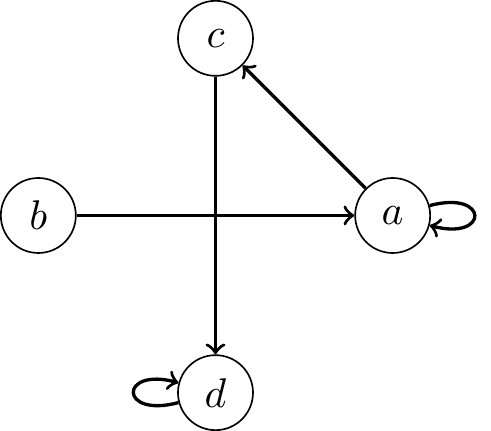
It is often helpful to visualize a relation by drawing arrows between the items that are related. To visualize \(R \subseteq X \times X\), begin by writing down all the elements of \(X\). Then, for each \((x, y) \in R\), draw an arrow from element \(x\) to element \(y\).

For example, suppose \(X = \{a, b, c, d\}\) and \(R = \{(a,a), (b,a), (c,d), (a,c), (d,d)\}\). The relation \(R\) can be visualized as follows:

2.2 Properties of Relations

Typically, we are interested in relations satisfying special properties. Suppose that \(R\subseteq X\times X\). The following properties of \(R\) will be discussed this semester:

\(R\) is reflexive provided that for all \(a\in X\), \(a\mathrel{R} a\).
\(R\) is irrfelexive provided that for all \(a\in X\), it is not the case that \(a\mathrel{R} a\).
\(R\) is symmetric provided that for all \(a,b\in X\), if \(a\mathrel{R} b\) then \(b\mathrel{R} a\).
\(R\) is asymmetric provided that for all \(a,b\in X\), if \(a\mathrel{R}b\) then it is not the case that \(b\mathrel{R} a\).
\(R\) is transitive provided that for all \(a,b,c\in X\), if \(a\mathrel{R} b\) and \(b\mathrel{R} c\) then \(a\mathrel{R} c\).

The following tutorial gives you a chance to practice identifying properties of relations: https://epacuit-relation-properties-relation-properties-q9wf83.streamlitapp.com

2.3 Cycles

We will often use the following shorthand to represent elements in a relation: If \(x_1, \ldots, x_n \in X\), then \[x_1\mathrel{R} x_2\mathrel{R}\cdots x_{n-1}\mathrel{R}x_n\] means that for all \(i = 1, \ldots, n-1\), \((x_i, x_{i+1}) \in R\). If \(R\) is assumed to be transitive, this notation implies that \((x_i, x_j) \in R\) for all \(j < i\), or for all \(j \leq i\) if \(R\) is also reflexive.

For example, if \(R\) is both transitive and reflexive, then \(a \mathrel{R} b \mathrel{R} c\) means that the set \(\{(a, a), (a, b), (b, b), (a, c), (b, c), (c, c)\} \subseteq R\).

Suppose that \(R\) is a relation on \(X\). A path in \(R\) is a sequence of elements \(x_1, x_2, \ldots, x_n\in X\) such that each element of the sequence is \(R\)-related to the next element. That is, \[x_1\mathrel{R} x_2\mathrel{R} x_3\mathrel{R}\cdots x_{n-1} \mathrel{x_n}\]

When the last element of a path is also related to the first elements, we call the path a cycle.

Definition 2.3 (Cycle) Suppose that \(R\subseteq X\times X\). A (simple) cycle in \(R\) is a sequence of distinct elements \((x_1, x_2,\ldots, x_n)\) such that \(x_i\in X\) for all \(i=1, \ldots, n\) and for all \(i=1, \ldots, n-1\), \(\ x_i \mathrel{R} x_{i+1}\), and \(x_n\mathrel{R} x_1\). A relation \(R\) is said to be acyclic if there are no cycles.

For example, suppose that \(X=\{a,b,c, d\}\) and \(R=\{(a,c), (b,a), (b,d), (c, b), (d, c), (d, a)\}\). This relation can be pictured as follows:

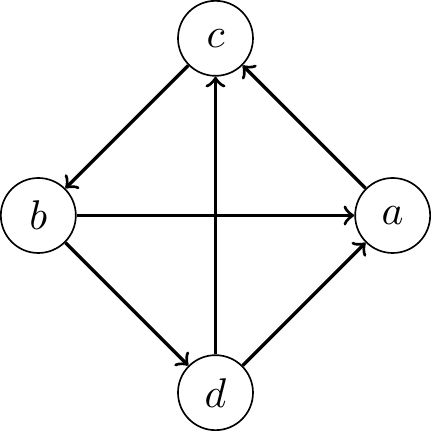
There are 3 cycles in \(R\):

\((a,c,b)\)
\((c,b,d)\)
\((c,b,d,a)\).

This examples demonstrates that:

A relation \(R\subseteq X\times X\) may have multiple cycles; and
A cycle in a \(R\subseteq X\times X\) need not involve all elements of \(X\).

2.4 Exercises

Suppose that \(A=\{b,c\}\) and \(B=\{2,3\}\). Find all the following sets.
1. \(A\times B\)
2. \(B \times A\)
3. \(A\times A\)
4. \(B\times B\)
5. \((A\times A)\times B\)
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,a), (b,c), (a,c)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Transitive
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a, b), (b, c), (c, a), (a, a), (b, b), (c, c)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Transitive
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b), (b, c), (a,c)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Transitive
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Transitive
What properties does the relation \(\geq\) on numbers satisfy?
What properties does the relation \(>\) on numbers satisfy?
Give an example of a relation on people that satisfies:
1. transitivity and symmetry.
2. symmetry but not transitivity.
3. transitivity but not symmetry.
List all the cycles in the relation \(R=\{(a, b), (a, c), (a, d), (b, c), (c, d), (d, b)\}\).
Can you find an example of a relation that is transitive, symmetric but not reflexive?

Solutions

Suppose that \(A=\{b,c\}\) and \(B=\{2,3\}\). Find all the following sets.
1. \(A\times B = \{(b, 2), (b, 3), (c, 2), (c, 3)\}\)
2. \(B \times A = \{(2, b), (2, c), (3, b), (3, c)\}\)
3. \(A\times A = \{(b, b), (b, c), (c, b), (c, c)\}\)
4. \(B\times B = \{(2, 2), (2, 3), (3, 2), (3, 3)\}\)
5. \((A\times A)\times B = \{(b, b, 2), (b, c, 2), (c, b, 2), (c, c, 2), (b, b, 3), (b, c, 3), (c, b, 3), (c, c, 3)\}\)
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,a), (b,c), (a,c)\}\). What properties does \(R\) satisfy?
1. \(R\) is not reflexive since \((b,b)\not\in R\).
2. \(R\) is not symmetric since \((b,c)\in R\), but \((c,b)\not\in R\).
3. \(R\) is not asymmetric since \((a,a)\in R\).
4. \(R\) is transitive.
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a, b), (b, c), (c, a), (a, a), (b, b), (c, c)\}\). What properties does \(R\) satisfy?
1. \(R\) is reflexive.
2. \(R\) is not symmetric since \((b,c)\in R\), but \((c,b)\notin R\).
3. \(R\) is not asymmetric since \((a,a)\in R\).
4. \(R\) is not transitive since \((a, b)\in R\), \((b, c)\in R\), but \((a, c)\notin R\).
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b), (b, c), (a,c)\}\). What properties does \(R\) satisfy?
1. \(R\) is not reflexive since \((a,a)\not\in R\).
2. \(R\) is not symmetric since \((b,c)\in R\), but \((c,b)\not\in R\).
3. \(R\) is asymmetric.
4. \(R\) is transitive.
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b)\}\). What properties does \(R\) satisfy?
1. \(R\) is not reflexive since \((a,a)\not\in R\).
2. \(R\) is not symmetric since \((a,b)\in R\), but \((b,a)\not\in R\).
3. \(R\) is asymmetric.
4. \(R\) is transitive.
What properties does the relation \(\geq\) on numbers satisfy?

\(\geq\) is transitive, and reflexive. \(\geq\) is not symmetric since \(2 \geq 1\) but \(1\not\geq 2\), and it is not asymmetric since \(1\geq 1\).
What properties does the relation \(>\) on numbers satisfy?

\(>\) is transitive and asymmetric. \(>\) is not reflexive since \(1\not > 1\), it is not symmetric since \(2 > 1\) but \(1\not > 2\).
Give an example of a relation on people that satisfies:
1. transitivity and symmetry: Consider the relation \(R\) in which a person \(a\) is related to a person \(b\) when \(a\) and \(b\) have the same last name. (If \(a\) hs the same last name as \(b\), then \(b\) has the same last name as \(a\), and if \(a\) has the same last name as \(b\) and \(b\) has the same last name as \(c\), then \(a\) and \(c\) must have the same last name.)
2. symmetry but not transitivity: Consider the relation \(R\) in which a person \(a\) is related to a person \(b\) and \(a\) and \(b\) shake hands. Clearly, if \(a\) shakes hands with \(b\), then \(b\) also shakes hands with \(a\). Suppose that there is a room three people, Ann, Bob, and Charles. Suppose that Ann and Bob shake hands, and Bob and Charles shake hands, but Ann does not shake hands with Charles. This shows that the “shake-hands” relation need not be transitive.
3. transitivity but not symmetry: Consider the “taller-than” relation in which \(a\) is related to \(b\) when \(a\) is taller than \(b\). It is not hard to see that “taller-than” is transitive, but not symmetric.
List all the cycles in the relation \(R=\{(a, b), (a, c), (a, d), (b, c), (c, d), (d, b)\}\).

There is one cycle in this relation: \((b, c, d)\).
Can you find an example of a relation that is transitive, symmetric but not reflexive?

This is tricky. First of all, note that the empty relation \(R=\varnothing\) on a non-empty set \(X\) is trivially transitive, symmetric, but is not reflexive.

However, if \(R\) is non-empty, then if \(R\) is transitive and symmetric, then it is reflexive. Suppose that \((a,b)\in R\). Then, by symmetric \((b, a)\in R\) and by transitivity, \((a, a)\in R\).