2 Relations

The order of the elements in a set does not matter. That is, \(\{a, b\}\) is the same set as \(\{b, a\}\) (they both denote the set consisting of two elements \(a\) and \(b\)). Similarly, listing the same element multiple times does not change a set. So, for instance, \(\{a,a,b\}\) is the same set as \(\{a,b\}\).

We use ‘\((\)’ and ‘\()\)’ when the order of elements is important. For instance, \((a,b)\) is called an ordered pair, or tuple of length 2. The first component is \(a\) and the second component is \(b\). Since the order in which the elements appear matters, we have that \((a, b)\ne (b,a)\). While there is only one set containing the two elements \(a\) and \(b\), there are 4 different ordered pairs that can be constructed using the elements \(a\) and \(b\): \[(a, a) \qquad (a, b)\qquad (b, a) \qquad (b, b).\]

Definition 2.1 (Product) Suppose that \(A\) and \(B\) are non-empty sets. The product of \(A\) and \(B\), denoted \(A\times B\), is the set of ordered pairs where the first component comes from \(A\) and the second component comes from \(B\). That is,

\[A\times B=\{(a,b)\ |\ a\in A\text{ and } b\in B\}.\]

Suppose that \(X=\{a, b, c\}\) and \(Y=\{1, 2\}\). Then we have the following:

\(X\times Y=\{(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)\}.\)
\(Y\times X=\{(1,a), (1,b), (1,c), (2,a), (2,b), (2,c)\}.\)
\(X\times X=\{(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)\}.\)

Tuples of length greater than 2

Suppose that \(X=\{a, b\}\) and \(Y=\{d, e\}\), we have that \((X\times X)\times Y\) is \[\{((a,a),d), ((a,b),d), ((b, a),d), ((b,b),d), ((a,a),e), ((a,b),e), ((b, a),e), ((b,b),e)\}.\]

So, elements of \((X\times X) \times Y\) are tuples where the first component is a tuple of length 2 (where each component is from \(X\)) and the second component is an element of \(Y\). Often we will drop the parentheses, writing \(X\times X\times Y\), and view the elements of this set as tuples of length 3:

\[\{(a,a,d), (a,b,d), (b,a,d), (b,b,d), (a,a,e), (a,b,e), (b,a,e), (b,b,e)\}.\]

The parentheses can be recovered by associating them to the left.

Definition 2.2 (Relation) A relation on a set \(X\) is a subset of \(X\times X\) (the set of pairs of elements from \(X\)). That is, if \(R\subseteq X\times X\), then \(R\) is a relation on \(X\).

Relations are an important mathematical tool used throughout Philosophy, Political Science, and Economics. You have already studied binary relations during your mathematical eduction: \(=,\le, \ge, <,\) and \(>\) are all relations on numbers (e.g., the natural numbers \(\mathbb{N}\), real numbers \(\mathbb{R}\), rational numbers \(\mathbb{Q}\), etc.) and \(\subseteq\) is a relation on the power set of a set. For example, the binary relation \(\ge \subseteq \mathbb{N}\times \mathbb{N}\) is the set

\[\{(a,b)\ |\ a,b\in\mathbb{N}\text{ and } a\text{ is greater than or equal to } b\}.\]

2.1 Notation

Given a set \(R\subseteq X\times X\) of ordered pairs, \((a,b)\in R\) represents that \(a\) is related to \(b\) according to \(R\), and if \((a, b)\notin R\), then \(a\) is not related to \(b\) according to \(R\). To simplify notation, we write \(a\mathrel{R} b\) when \((a, b)\in R\). The following is a summary of the notation you will use this semester:

Mathematical Notation	Meaning
\((a, b)\in R\)	\(a\) is related to \(b\) according to \(R\).
\(a\mathrel{R} b\)	\(a\) is related to \(b\) according to \(R\).
\((a, b)\notin R\)	\(a\) is not related to \(b\) according to \(R\).
not-\(a\mathrel{R} b\)	\(a\) is not related to \(b\) according to \(R\).
\(a\mathrel{R\mkern-9.75mu/} b\)	\(a\) is not related to \(b\) according to \(R\).

For instance, we can express that \(4\) is greater-than-or-equal-to \(1\) by writing \(4\geq 1\) or \((4, 1)\in \geq\), and that \(2\) is not greater-than-or-equal-to \(3\) by writing \(2\not\geq 3\) or \((2,3)\notin\geq\).

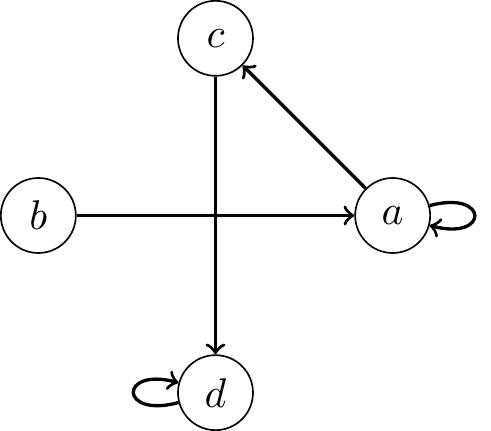
Often it is useful to visualize a relation by drawing arrows between items that are related. To visualize \(R\subseteq X\times X\), write down all the elements of \(X\) and then for each \((x, y)\in R\) draw an arrow from element \(x\) to element \(y\). For example, suppose that \(X=\{a,b,c,d\}\) and \(R=\{(a,a), (b,a), (c,d), (a,c), (d,d)\}\). Then \(R\) is visualized as follows:

For instance, consider the relation \(\geq\subseteq \mathbb{N}\times\mathbb{N}\) of “greater-than-or-equal-to”. Then, we have that \((4, 1)\in \geq\) since \(4\) is greater-than-or-equal-to \(1\) and \((2, 3)\notin \geq\) since \(2\) is not greater-than-or-equal-to \(3\).

We will often use the following shorthand to denote elements in the relation: If \(x_1, \ldots, x_n\in X\), then

\[x_1\mathrel{R} x_2\mathrel{R}\cdots x_{n-1}\mathrel{R}x_n\]

means that for all \(i=1,\ldots, n-1\), \((x_i,x_{i+1})\in R\) or \((x_i,x_j)\in R\) for all \(j< i\) if \(R\) is assumed to be transitive (or \(j\le i\) if \(R\) is assumed to also be reflexive). For example, if \(R\) is transitive and reflexive, then \(a\mathrel{R} b\mathrel{R} c\) means that \(\{(a,a), (a,b), (b,b), (a,c), (b,c), (c,c)\}\subseteq R\).

2.2 Lecture

2.3 Properties of Relations

Typically, we are interested in relations satisfying special properties. Suppose that \(R\subseteq X\times X\). The following properties of \(R\) will be discussed this semester:

\(R\) is reflexive provided that for all \(a\in X\), \(a\mathrel{R} a\).
\(R\) is connected provided that for all \(a,b\in X\), \(a\mathrel{R} b\) or \(b\mathrel{R} a\) (or both). A connected relation is also called complete.
\(R\) is symmetric provided that for all \(a,b\in X\), if \(a\mathrel{R} b\) then \(b\mathrel{R} a\).
\(R\) is asymmetric provided that for all \(a,b\in X\), if \(a\mathrel{R}b\) then it is not the case that \(b\mathrel{R} a\).
\(R\) is transitive provided that for all \(a,b,c\in X\), if \(a\mathrel{R} b\) and \(b\mathrel{R} c\) then \(a\mathrel{R} c\).

Note

As stated, connectedness implies reflexivity (let \(a=b\) in the definition of connected). Sometimes, connectedness is defined as follows: for all distinct \(a,b\in X\), \(a\mathrel{R} b\) or \(b\mathrel{R} a\). In what follows, we will use the above stronger definition of connected where all connected relations are reflexive.

The following tutorial gives you a chance to practice identifying properties of relations: https://epacuit-relation-properties-relation-properties-q9wf83.streamlitapp.com

2.4 Cycles

Suppose that \(R\) is a relation on \(X\). A path in \(R\) is a sequence of elements \(x_1, x_2, \ldots, x_n\in X\) such that each element of the sequence is \(R\)-related to the next element. That is, \[x_1\mathrel{R} x_2\mathrel{R} x_3\mathrel{R}\cdots x_{n-1} \mathrel{x_n}\]

When the last element of a path is also related to the first elements, we call the path a cycle.

Definition 2.3 (Cycle) Suppose that \(R\subseteq X\times X\). A (simple) cycle in \(R\) is a sequence of distinct elements \((x_1, x_2,\ldots, x_n)\) such that \(x_i\in X\) for all \(i=1, \ldots, n\) and for all \(i=1, \ldots, n-1\), \(\ x_i \mathrel{R} x_{i+1}\), and \(x_n\mathrel{R} x_1\). A relation \(R\) is said to be acyclic if there are no cycles.

For example, suppose that \(X=\{a,b,c, d\}\) and \(R=\{(a,c), (b,a), (b,d), (c, b), (d, c), (d, a)\}\). This relation can be pictured as follows:

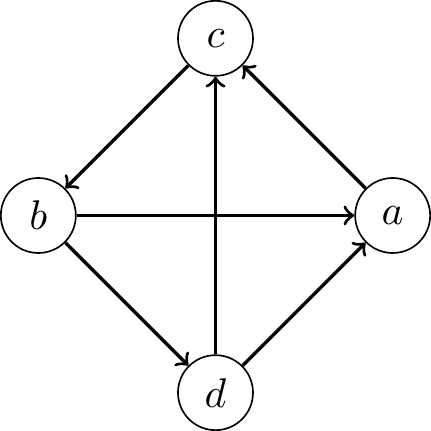
There are 3 cycles in \(R\):

\((a,c,b)\)
\((c,b,d)\)
\((c,b,d,a)\).

This examples demonstrates that:

A relation \(R\subseteq X\times X\) may have multiple cycles; and
A cycle in a \(R\subseteq X\times X\) need not involve all elements of \(X\).

2.5 Exercises

Suppose that \(A=\{b,c\}\) and \(B=\{2,3\}\). Find all the following sets.
1. \(A\times B\)
2. \(B \times A\)
3. \(A\times A\)
4. \(B\times B\)
5. \((A\times A)\times B\)
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,a), (b,c), (a,c)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Connected
5. Transitive
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a, b), (b, c), (c, a), (a, a), (b, b), (c, c)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Connected
5. Transitive
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b), (b, c), (a,c)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Connected
5. Transitive
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b)\}\). What properties does \(R\) satisfy?
1. Reflexive
2. Symmetric
3. Asymmetric
4. Connected
5. Transitive
What properties does the relation \(\geq\) on numbers satisfy?
What properties does the relation \(>\) on numbers satisfy?
Give an example of a relation on people that satisfies:
1. transitivity and symmetry.
2. symmetry but not transitivity.
3. transitivity but not symmetry.
List all the cycles in the relation \(R=\{(a, b), (a, c), (a, d), (b, c), (c, d), (d, b)\}\).
Can you find an example of a relation that is transitive, symmetric but not reflexive?

Solutions

Suppose that \(A=\{b,c\}\) and \(B=\{2,3\}\). Find all the following sets.
1. \(A\times B = \{(b, 2), (b, 3), (c, 2), (c, 3)\}\)
2. \(B \times A = \{(2, b), (2, c), (3, b), (3, c)\}\)
3. \(A\times A = \{(b, b), (b, c), (c, b), (c, c)\}\)
4. \(B\times B = \{(2, 2), (2, 3), (3, 2), (3, 3)\}\)
5. \((A\times A)\times B = \{(b, b, 2), (b, c, 2), (c, b, 2), (c, c, 2), (b, b, 3), (b, c, 3), (c, b, 3), (c, c, 3)\}\)
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,a), (b,c), (a,c)\}\). What properties does \(R\) satisfy?
1. \(R\) is not reflexive since \((b,b)\not\in R\).
2. \(R\) is not symmetric since \((b,c)\in R\), but \((c,b)\not\in R\).
3. \(R\) is not asymmetric since \((a,a)\in R\).
4. \(R\) is not connected since \((b,b)\not\in R\).
5. \(R\) is transitive.
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a, b), (b, c), (c, a), (a, a), (b, b), (c, c)\}\). What properties does \(R\) satisfy?
1. \(R\) is reflexive.
2. \(R\) is not symmetric since \((b,c)\in R\), but \((c,b)\notin R\).
3. \(R\) is not asymmetric since \((a,a)\in R\).
4. \(R\) is connected.
5. \(R\) is not transitive since \((a, b)\in R\), \((b, c)\in R\), but \((a, c)\notin R\).
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b), (b, c), (a,c)\}\). What properties does \(R\) satisfy?
1. \(R\) is not reflexive since \((a,a)\not\in R\).
2. \(R\) is not symmetric since \((b,c)\in R\), but \((c,b)\not\in R\).
3. \(R\) is asymmetric.
4. \(R\) is not connected since \((a,a)\not\in R\).
5. \(R\) is transitive.
Suppose that \(X=\{a, b, c\}\) and that \(R=\{(a,b)\}\). What properties does \(R\) satisfy?
1. \(R\) is not reflexive since \((a,a)\not\in R\).
2. \(R\) is not symmetric since \((a,b)\in R\), but \((b,a)\not\in R\).
3. \(R\) is asymmetric.
4. \(R\) is not connected since \((a,c)\not\in R\) and \((c,a)\not\in R\).
5. \(R\) is transitive.
What properties does the relation \(\geq\) on numbers satisfy?

\(\geq\) is transitive, reflexive, and connected. \(\geq\) is not symmetric since \(2 \geq 1\) but \(1\not\geq 2\), and it is not asymmetric since \(1\geq 1\).
What properties does the relation \(>\) on numbers satisfy?

\(>\) is transitive and asymmetric. \(>\) is not reflexive since \(1\not > 1\), it is not symmetric since \(2 > 1\) but \(1\not > 2\), and it is not connected since \(1 \not > 1\).
Give an example of a relation on people that satisfies:
1. transitivity and symmetry: Consider the relation \(R\) in which a person \(a\) is related to a person \(b\) when \(a\) and \(b\) have the same last name. (If \(a\) hs the same last name as \(b\), then \(b\) has the same last name as \(a\), and if \(a\) has the same last name as \(b\) and \(b\) has the same last name as \(c\), then \(a\) and \(c\) must have the same last name.)
2. symmetry but not transitivity: Consider the relation \(R\) in which a person \(a\) is related to a person \(b\) and \(a\) and \(b\) shake hands. Clearly, if \(a\) shakes hands with \(b\), then \(b\) also shakes hands with \(a\). Suppose that there is a room three people, Ann, Bob, and Charles. Suppose that Ann and Bob shake hands, and Bob and Charles shake hands, but Ann does not shake hands with Charles. This shows that the “shake-hands” relation need not be transitive.
3. transitivity but not symmetry: Consider the “taller-than” relation in which \(a\) is related to \(b\) when \(a\) is taller than \(b\). It is not hard to see that “taller-than” is transitive, but not symmetric.
List all the cycles in the relation \(R=\{(a, b), (a, c), (a, d), (b, c), (c, d), (d, b)\}\).

There is one cycle in this relation: \((b, c, d)\).
Can you find an example of a relation that is transitive, symmetric but not reflexive?

This is tricky. First of all, note that the empty relation \(R=\varnothing\) on a non-empty set \(X\) is trivially transitive, symmetric, but is not reflexive.

However, if \(R\) is non-empty, then if \(R\) is transitive and symmetric, then it is reflexive. Suppose that \((a,b)\in R\). Then, by symmetric \((b, a)\in R\) and by transitivity, \((a, a)\in R\).